三 23 四月 2014

Filed under Machine Learning

Tags Machine Learning Exponential Family Generalized Linear Models

指数分布族

---

一件特别神奇的事是实际上我们学过或者用到的很多分布函数均可以写成一种一致的形式,事实上，属于这个家族的分布函数还是很多的，例如高斯分布、Bernoulli分布、二项分布、多项分布、指数分布、泊松分布、Dirichlet分布等,作为一个庞大家族的一员，这些分布函数具有一个它们引以为豪的共同的名字------指数分布族。以下我们就介绍一下指数分布族的基础知识吧。

定义

传说中的这个神奇的家族中的分一个分布函数均可写成如下形式:

\begin{equation} p(x) = h(x)e^{\theta^T T(x)-A(\theta)} \end{equation}

其中,$\theta$为参数向量,$T(x)$为"Sufficient statistics"向量,$A(\theta)$为cumulate generating function.

上式中我们不难注意到$\theta$和$x$仅在$\theta^T T(x)$一项中耦合在一起。另,指数分布族函数之积仍是指数分布族函数,只是可能不再具有良好的参数形式。

为了得到一个归一化的分布，我们有:对于任一$\theta$,

\begin{equation} \int p(x)dx = e^{-A(\theta)}\int h(x) e^{\theta^T T(x)} dx = 1 \end{equation}

即:

\begin{equation} e^{A(\theta)} = \int h(x) e^{\theta^T T(x)} dx \end{equation}

当$T(x)=x$时,$A(\theta)$是对于$h(x)$做拉普拉斯变换之后的$log$值。

以下我们举几个实例以使我们对其有一个更为清晰的认识:

Bernoulli Distribution

对于Bernoulli分布,我们有:

\begin{equation} \begin{split} p(x) &= \alpha^x (1-\alpha)^{1-x} \\ &= exp[log(\alpha^x (1-\alpha)^{1-x})] \\ &= exp[xlog \alpha + (1-x) log(1-\alpha)] \\ &= exp[xlog \frac{\alpha}{1-\alpha}+log(1-\alpha)] \\ &= exp[x\theta - log(1+e^{\theta})] \end{split} \end{equation}

于是我们有:

\begin{equation} \begin{split} T(x) &= x \\ \theta &= log \frac{\alpha}{1-\alpha} \\ A(\theta) &= log(1+e^{\theta}) \end{split} \end{equation}

Univariate Gaussian

对于单变量高斯分布,我们有:

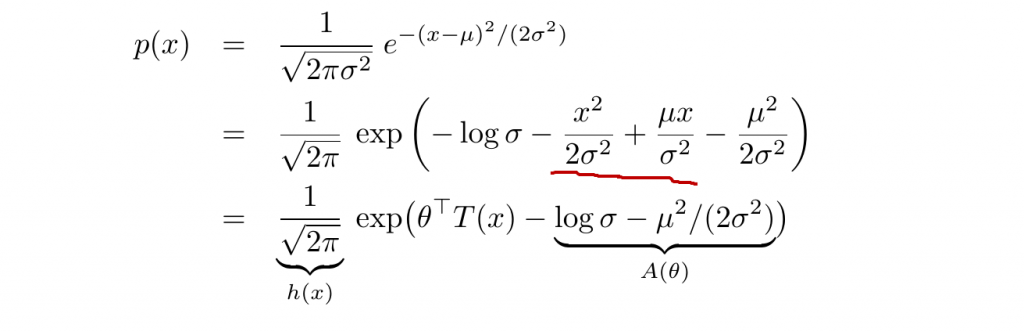
其中:

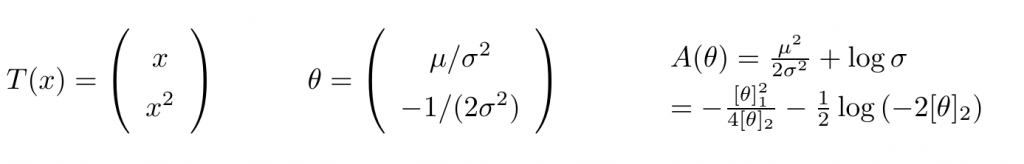
Multivariate Gaussian

对于形如下式的多变量高斯分布:

\begin{equation} p(x) = \frac{1}{(2\pi)^{D/2}|\Sigma|^{1/2}} e^{(x-\mu)^T \Sigma^{-1} (x-\mu)/2} \end{equation}

我们有:(下式我并未真正推导)

\begin{equation} \begin{split} h(x) &= (2\pi)^{-D/2} \\ T(x) &= \left( \begin{array}{cc} x \\ xx^T \end{array} \right) \\ \theta &= \left( \begin{array}{cc} \Sigma^{-1}\mu \\ -{1 \over 2}\Sigma^{-1} \end{array} \right) \end{split} \end{equation}

一阶导数

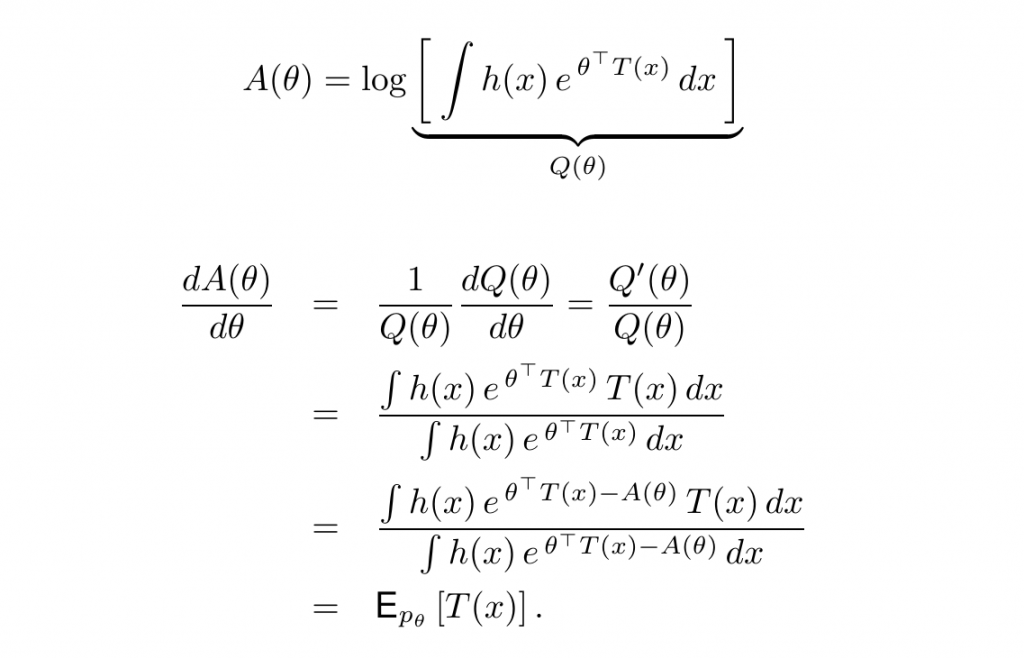
二阶导数

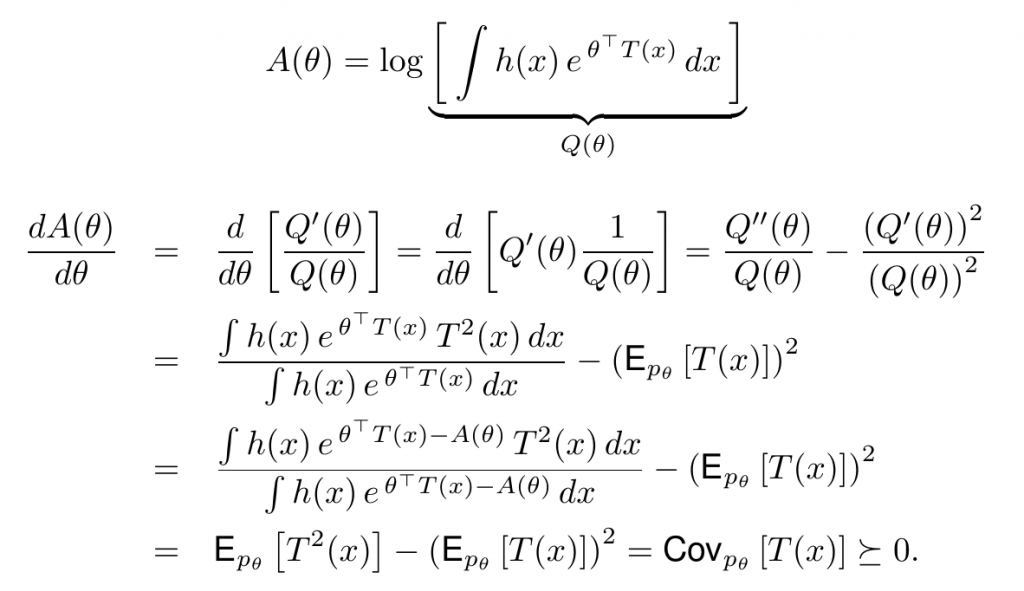
即$A(\theta)$是凸的($\succeq$表示正定positive definite)

Maximum Likelihood

根据$p(x)$的定义,我们有:

\begin{equation} l(\theta) = \sum_{i=1}^{N} log p(x_i|\theta) = \sum_{i=1}^{N} [log h(x_i) + \theta^T T(x_i) - A(\theta)] \end{equation}

为了求得极大似然解,我们对$\theta$求偏导有:

\begin{equation} l \prime(\theta) = [\sum_{i=1}^N T(x_i)] - NA\prime(\theta) = 0 \end{equation}

于是我们有:

\begin{equation} A\prime(\hat\theta_{ML})=\frac{1}{N} \sum_{i=1}^N T(x_i) \end{equation}

Conjugate Priors in Bayesian Statistics

根据Bayes Rule,我们有:

\begin{equation} p(\theta|x) = \frac{p(x|\theta)p(\theta)}{\int p(x|\theta)p(\theta) d\theta} \end{equation}

NOTE:分母项只是一归一化项,其值与$\theta$无关。于是我们有$p(\theta|x) \propto p(x|\theta)p(\theta)$.

正如我们之前提到的那样，为了简化计算,我们最好使得先验分布$p(\theta)$与Marginal Likelihood $p(x|\theta)$具有相似的形式(此时它们成为共轭分布)。如当先验分布是Dirichlet分布时,当我们取Marginal Likelihood为多项式分布时,后验分布为Dirichlet分布。由于Dirichlet分布与多项式分布具有相似的形式,在一定程度上可以简化我们的计算。

NOTE:关于Dirichlet与Multinomial之间的关系我们会在之后的Dirichlet Process一篇中详细展开,敬请期待,此处不再赘述。

常见的共轭分布如下表所示:

广义线性模型

---

从软件工程的视角来看,如果我们把广义线性模型(Generalized Linear Models,GLM)看作一个类,线性回归与Logistic回归只不过是该类的两个实例而已,由此可见GLM是一个较为高大上的东东啊!以下对其进行一个较为简单的介绍:

基础知识

为了理解GLM,我们首先引入:

\begin{equation} p(y_i|\theta,\sigma^2) = exp[\frac{y_i\theta-A(\theta)}{\sigma^2}+c(y_i,\sigma^2)] \end{equation}

其中,$\sigma^2$为dispersion parameter(一般设置为1),$\theta$为自然参数,$A$为partition function,$c$为归一化常数.如对于Logistic Regression而言,$\theta$为log-odds ratio,$\theta = log(\frac{\mu}{1-\mu})$,其中$\mu = E[y] = p(y=1)$为mean.为了将mean转化为自然参数,我们引入函数$\psi$,有:$\theta = \mathbf \Psi(\mu)$.实际上,如果存在逆向映射,我们则有:$\mu = \mathbf \Psi^{-1}(\theta)$.此外,根据我们以上推导的$A(\theta)$的一阶导数知:

\begin{equation} \mu = \Psi^{-1}(\theta) = A\prime(\theta) \end{equation}

若我们令:

\begin{equation} \eta_i = w^T x_i \end{equation}

我们可以定义如下mean function,记为$g^{-1}$,使得:

\begin{equation} \mu_i = g^{-1}(\eta_i) = g^{-1}(w^T x_i) \end{equation}

Mean function的逆函数,即$g()$,则称为Link function.我们可以选取任意函数作为$g()$,只要它是可逆的,且使得逆函数具有合适的取值范围。如针对Logistic Regression而言,我们有:$\mu_i = g^{-1}(\eta_i) = sigm(\eta_i)$

一种最为简单的Link function的函数是取$g=\psi$,称为Canonical Link Function.上面我们定义$\theta_i = \eta_i = w^Tx_i$,于是模型变为:

\begin{equation} p(y_i|x_i,w,\sigma^2) = exp[\frac{y_iw^Tx_i-A(w^Tx_i)}{\sigma^2}+c(y_i,\sigma^2)] \end{equation}

下表中,我们给出一些常见分布函数及其对应的Canonical Link Functions.我们可以看到对于Bernoulli和二项分布而言,Canonical Link Function为logit函数,$g(\mu)=log(\frac{\eta}{1-\eta})$,其逆函数为logistic函数,$\mu = sigm(\eta)$.

根据我们第一部分对一阶导数以及二阶导数的推导我们有:

\begin{equation} \begin{split} E[y|x_i,w,\sigma^2] &= \mu_i = A\prime(\theta_i) \\ var[y|x_i,w,\sigma^2] &= \sigma_i^2 = A\prime\prime(\theta_i)\sigma^2 \end{split} \end{equation}

为了更便于理解,我们举几个具体的例子:

• 对于线性回归而言,我们有:

\begin{equation} log p(y_i|x_i,w,\sigma^2) = \frac{y_i\mu_i-\frac{\mu_i^2}{2}}{\sigma^2} - {1 \over 2}(\frac{y_i^2}{\sigma_i^2}+log(2\pi \sigma^2)) \end{equation}

其中,$y_i \in R$,且$\theta_i = \mu_i = w^T x_i$,这里我们取$A(\theta) = \theta^2/2$,因此$E[y_i] = \mu_i$,且$var[y_i]=\sigma^2$.

• 对于二项分布而言,我们有:(后面这两个未证明结论的正确性)

\begin{equation} log p(y_i|x_i,w) = y_i log(\frac{\pi_i}{1-\pi_i}) +N_ilog(1-\pi_i)+log \left( \begin{array}{cc} N_i \\ y_i \end{array} \right) \end{equation}

其中,$y_i \in {0,1,...,N_i}$,$\pi_i = sigm(w^Tx_i)$,$\theta_i = log(\pi_i/(1-\pi_i))=w^Tx_i$，且$\sigma^2=1$.这里我们取$A(\theta) = N_ilog(1+e^{\theta})$.于是我们有$E[y_i] = N_i \pi_i=\mu_i$,$var[y_i] = N_i \pi_i (1-\pi_i)$.

• 对于Poisson Regression而言,我们有:

\begin{equation} log p(y_i|x_i,w) = y_i log \mu_i - \mu_i - log(y_i!) \end{equation}

其中,$y_i \in {0,1,2,...}$,$\mu_i = exp(w^Tx_i)$,$\theta_i = log(\mu_i) = w^Tx_i$且$\sigma^2=1$.这里我们取$A(\theta) = e^{\theta}$,于是我们有$E[y_i] = var[y_i] = \mu_i$.

MLE Estimation

其极大似然函数具有如下形式:

\begin{equation} \begin{split} \ell(w) = log p(D|w) &= \frac{1}{\sigma^2}\sum_{i=1}^N \ell_i \\ \ell_i &\triangleq \theta_iy_i-A(\theta_i) \end{split} \end{equation}

我们可通过下式计算其梯度向量:

\begin{equation} \begin{split} \frac{\ell_i}{w_j} &= \frac{\ell_i}{\theta_i}\frac{\theta_i}{\mu_i}\frac{\mu_i}{\eta_i}\frac{\eta_i}{w_j} \\ &= (y_i - A\prime(\theta_i))\frac{\theta_i}{\mu_i}\frac{\mu_i}{\eta_i}x_{ij} \\ &= (y_i-\mu_i)\frac{\theta_i}{\mu_i}\frac{\mu_i}{\eta_i}x_{ij} \end{split} \end{equation}

如果我们采用Canonical Link Function,$\theta_i = \eta_i$,上式可简化为:

\begin{equation} \bigtriangledown_w \ell(w) = \frac{1}{\sigma^2}[\sum_{i=1}^N (y_i-\mu_i)x_i] \end{equation}

利用该结果执行梯度下降即可得到ML估计值。

TODO Board:

• Probit Regression
• Multi-task Learning(Transfer Learning)
• Generalized Linear Mixture Models
• Learning to rank

参考文献

---

1. Exponential Family

---