一 14 四月 2014

Filed under Pearls

Tags 基数估计 Cardinality Estimation Big Data

记得之前某周例会的时候一个博士师兄抛出一个小问题:在大数据环境下,如何估计一个可能含有重复元素的集合中不同元素的数目,当时其实没有怎么在意。这两天因为看CNN的东西实在无法完全理解,所以到处逛了逛(好吧,我每次逛了逛都能发现特别好玩的算法呀),于是不经意间发现了解决上述问题的一些现有算法,很是高兴呀。

在开始今天的相关介绍之前,咱们扯点闲话吧,个人不是特别喜欢纯科研的科研,如果一个算法或者一个数据结构以至于一个理论不能应用到实际生活中去,不能解决实际生活中的某个问题的话,个人认为这种理论或者算法/数据结构的研究就是无意义的。个人还是比较倾向于好玩的科研吧,一方面研究的东西自己觉得有意思,另一方面又能应用到实际项目或生活实际中去,成为一个研究好玩问题的研究人员估计就是我毕生最大的志向了吧,呵呵。好吧,其实说这么多只是为了说明基数估计这个东西真的很好玩呀。(以后只要在Pearls目录下的博文均收集自他人博客,原始链接见脚注,版权属于原作者所有,无意侵犯,特此说明,以后不再说明)

言归正传,开始我们正式的介绍。

基本概念¹

---

基数计数(Cardinality Counting）是实际应用中一种常见的计算场景，在数据分析、网络监控及数据库优化等领域都有相关需求。精确的基数计数算法由于种种原因，在面对大数据场景时往往力不从心，因此如何在误差可控的情况下对基数进行估计就显得十分重要。目前常见的基数估计算法有Linear Counting、LogLog Counting、HyperLogLog Counting及Adaptive Counting等。这几种算法都是基于概率统计理论所设计的概率算法，它们克服了精确基数计数算法的诸多弊端（如内存需求过大或难以合并等），同时可以通过一定手段将误差控制在所要求的范围内。

以下我们主要介绍一下基数估计(Cardinality Estimation)的基本概念。

基数的定义

简单来说，基数（Cardinality，也译作势），是指一个集合（这里的集合允许存在重复元素，与集合论对集合严格的定义略有不同，如不做特殊说明，本文中提到的集合均允许存在重复元素）中不同元素的个数。例如看下面的集合：

${1,2,3,4,5,2,3,9,7}$

这个集合有9个元素，但是2和3各出现了两次，因此不重复的元素为1,2,3,4,5,9,7，所以这个集合的基数是7。

如果两个集合具有相同的基数，我们说这两个集合等势。基数和等势的概念在有限集范畴内比较直观，但是如果扩展到无限集则会比较复杂，一个无限集可能会与其真子集等势（例如整数集和偶数集是等势的）。不过在这个系列文章中，我们仅讨论有限集的情况，关于无限集合基数的讨论，有兴趣的同学可以参考实变分析相关内容。

容易证明，如果一个集合是有限集，则其基数是一个自然数。

基数的应用实例

下面通过一个实例说明基数在电商数据分析中的应用。

假设一个淘宝网店在其店铺首页放置了10个宝贝链接，分别从Item01到Item10为这十个链接编号。店主希望可以在一天中随时查看从今天零点开始到目前这十个宝贝链接分别被多少个独立访客点击过。所谓独立访客（Unique Visitor，简称UV）是指有多少个自然人，例如，即使我今天点了五次Item01，我对Item01的UV贡献也是1，而不是5。

用术语说这实际是一个实时数据流统计分析问题。

要实现这个统计需求。需要做到如下三点：

1. 对独立访客做标识
2. 在访客点击链接时记录下链接编号及访客标记
3. 对每一个要统计的链接维护一个数据结构和一个当前UV值，当某个链接发生一次点击时，能迅速定位此用户在今天是否已经点过此链接，如果没有则此链接的UV增加1

下面分别介绍三个步骤的实现方案

对独立访客做标识

客观来说，目前还没有能在互联网上准确对一个自然人进行标识的方法，通常采用的是近似方案。例如通过登录用户+cookie跟踪的方式：当某个用户已经登录，则采用会员ID标识；对于未登录用户，则采用跟踪cookie的方式进行标识。为了简单起见，我们假设完全采用跟踪cookie的方式对独立访客进行标识。

记录链接编号及访客标记

这一步可以通过Javascript埋点及记录accesslog完成，具体原理和实现方案可以参考博文网站统计中的数据收集原理及实现。

实时UV计算

可以看到，如果将每个链接被点击的日志中访客标识字段看成一个集合，那么此链接当前的UV也就是这个集合的基数，因此UV计算本质上就是一个基数计数问题。

在实时计算流中，我们可以认为任何一次链接点击均触发如下逻辑（伪代码描述）：

cand_counting(item_no, user_id) {
    if (user_id is not in the item_no visitor set) {
        add user_id to item_no visitor set;
        cand[item_no]++;
    }
}

逻辑非常简单，每当有一个点击事件发生，就去相应的链接被访集合中寻找此访客是否已经在里面，如果没有则将此用户标识加入集合，并将此链接的UV加1。

虽然逻辑非常简单，但是在实际实现中尤其面临大数据场景时还是会遇到诸多困难，下面一节我会介绍两种目前被业界普遍使用的精确算法实现方案，并通过分析说明当数据量增大时它们面临的问题。

传统的基数计数实现

接着上面的例子，我们看一下目前常用的基数计数的实现方法。

基于B树的基数计数

对上面的伪代码做一个简单分析，会发现关键操作有两个：查找-迅速定位当前访客是否已经在集合中，插入-将新的访客标识插入到访客集合中。因此，需要为每一个需要统计UV的点（此处就是十个宝贝链接）维护一个查找效率较高的数据结构，又因为实时数据流的关系，这个数据结构需要尽量在内存中维护，因此这个数据结构在空间复杂度上也要比较适中。综合考虑一种传统的做法是在实时计算引擎采用了B树来组织这个集合。下图是一个示意图：

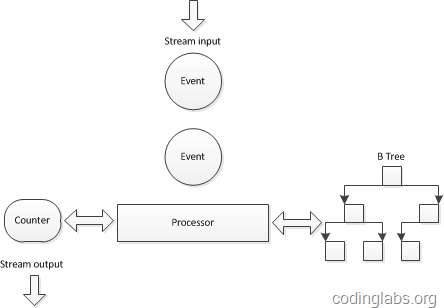
之所以选用B树是因为B树的查找和插入相关高效，同时空间复杂度也可以接受（关于B树具体的性能分析请参考B_Tree）。

这种实现方案为一个基数计数器维护一棵B树，由于B树在查找效率、插入效率和内存使用之间非常平衡，所以算是一种可以接受的解决方案。但是当数据量特别巨大时，例如要同时统计几万个链接的UV，如果要将几万个链接一天的访问记录全部维护在内存中，这个内存使用量也是相当可观的（假设每个B树占用1M内存，10万个B树就是100G！）。一种方案是在某个时间点将内存数据结构写入磁盘（双十一和双十二大促时一淘数据部的效果平台是每分钟将数据写入HBase）然后将内存中的计数器和数据结构清零，但是B树并不能高效的进行合并，这就使得内存数据落地成了非常大的难题。

另一个需要数据结构合并的场景是查看并集的基数，例如在上面的例子中，如果我想查看Item1和Item2的总UV，是没有办法通过这种B树的结构快速得到的。当然可以为每一种可能的组合维护一棵B树。不过通过简单的分析就可以知道这个方案基本不可行。N个元素集合的非空幂集数量为2N−1，因此要为10个链接维护1023棵B树，而随着链接的增加这个数量会以幂指级别增长。

基于Bitmap的基数计数

为了克服B树不能高效合并的问题，一种替代方案是使用Bitmap表示集合。也就是使用一个很长的bit数组表示集合，将bit位顺序编号，bit为1表示此编号在集合中，为0表示不在集合中。例如“00100110”表示集合 {2，5，6}。bitmap中1的数量就是这个集合的基数。

显然，与B树不同Bitmap可以高效的进行合并，只需进行按位或（or）运算就可以，而位运算在计算机中的运算效率是很高的。但是Bitmap方式也有自己的问题，就是内存使用问题。

很容易发现，Bitmap的长度与集合中元素个数无关，而是与基数的上限有关。例如在上面的例子中，假如要计算上限为1亿的基数，则需要12.5M字节的Bitmap，十个链接就需要125M。关键在于，这个内存使用与集合元素数量无关，即使一个链接仅仅有一个1UV，也要为其分配12.5M字节。

由此可见，虽然Bitmap方式易于合并，却由于内存使用问题而无法广泛用于大数据场景。

Linear Counting²

---

通过上面的介绍我们知道传统的精确基数计数算法在数据量大时会存在一定瓶颈，瓶颈主要来自于数据结构合并和内存使用两个方面。因此出现了很多基数估计的概率算法，这些算法虽然计算出的结果不是精确的，但误差可控，重要的是这些算法所使用的数据结构易于合并，同时比传统方法大大节省内存。

作为本文的第二部分，我们讨论Linear Counting算法。

简介

Linear Counting（以下简称LC）在1990年的一篇论文“A linear-time probabilistic counting algorithm for database applications”中被提出。作为一个早期的基数估计算法，LC在空间复杂度方面并不算优秀，实际上LC的空间复杂度与上文中简单Bitmap方法是一样的（但是有个常数项级别的降低），都是$O(N_{max})$，因此目前很少单独使用LC。不过作为Adaptive Counting等算法的基础，研究一下LC还是比较有价值的。

基本算法

思路

LC的基本思路是：设有一哈希函数$H$，其哈希结果空间有$m$个值（最小值$0$，最大值$m-1$），并且哈希结果服从均匀分布。使用一个长度为$m$的Bitmap，每个bit为一个桶，均初始化为0，设一个集合的基数为$n$，此集合所有元素通过$H$哈希到Bitmap中，如果某一个元素被哈希到第$k$个比特并且第$k$个比特为$0$，则将其置为$1$。当集合所有元素哈希完成后，设Bitmap中还有$u$个bit为$0$。则：

\begin{equation} \hat{n}=−mlog_u m \end{equation}

为$n$的一个估计，且为最大似然估计（MLE）。

示意图如下：

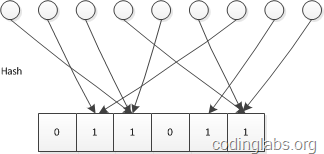
推导及证明

由上文对$H$的定义已知$n$个不同元素的哈希值服从独立均匀分布。设$A_j$为事件“经过$n$个不同元素哈希后，第$j$个桶值为0”，则：

\begin{equation} P(A_j)=(1−{1 \over m})n \end{equation}

又每个桶是独立的，则$u$的期望为：

\begin{equation} E(u)=\sum_{j=1}^mP(A_j)=m(1-\frac{1}{m})^n=m((1+\frac{1}{-m})^{-m})^{-n/m} \end{equation}

当$n$和$m$趋于无穷大时，其值约为$me^{-{n \over m}}$

令：

\begin{equation} E(u)=me^{-n/m} \end{equation}

得：

\begin{equation} n=−mlog \frac{E(u)}{m} \end{equation}

显然每个桶的值服从参数相同0-1分布，因此$u$服从二项分布。由概率论知识可知，当$n$很大时，可以用正态分布逼近二项分布，因此可以认为当$n$和$m$趋于无穷大时$u$渐进服从正态分布。

因此$u$的概率密度函数为：

\begin{equation} f(x) = {1 \over \sigma\sqrt{2\pi} }\,e^{- {{(x-\mu )^2 \over 2\sigma^2}}} \end{equation}

由于我们观察到的空桶数$u$是从正态分布中随机抽取的一个样本，因此它就是$\mu$的最大似然估计（正态分布的期望的最大似然估计是样本均值）。

又由如下定理：

设$f(x)$是可逆函数,$\hat{x}$是$x$的最大似然估计，则$f(\hat{x})$是$f(x)$的最大似然估计。 且$-mlog\frac{x}{m}$是可逆函数，则$\hat{n}=-mlog\frac{u}{m}$是$-mlog\frac{E(u)}{m}=n$的最大似然估计。

偏差分析

下面不加证明给出如下结论：

\begin{equation} \begin{split} Bias(\frac{\hat{n}}{n}) &=E(\frac{\hat{n}}{n})-1=\frac{e^t-t-1}{2n} \\ StdError(\frac{\hat{n}}{n}) &=\frac{\sqrt{m}(e^t-t-1)^{1/2}}{n} \end{split} \end{equation}

其中$t=n/m$

NOTE:以上结论的推导在“A linear-time probabilistic counting algorithm for database applications”可以找到。

算法应用

在应用LC算法时，主要需要考虑的是Bitmap长度$m$的选择。这个选择主要受两个因素的影响：基数$n$的量级以及容许的误差。这里假设估计基数$n$的量级大约为$N$，允许的误差为$\epsilon$，则$m$的选择需要遵循如下约束。

误差控制

这里以标准差作为误差。由上面标准差公式可以推出，当基数的量级为$N$，容许误差为$\epsilon$时，有如下限制：

\begin{equation} m > \frac{e^t-t-1}{(\epsilon t)^2} \end{equation}

将量级和容许误差带入上式，就可以得出$m$的最小值。

满桶控制

由LC的描述可以看到，如果$m$比$n$小太多，则很有可能所有桶都被哈希到了，此时$u$的值为0，LC的估计公式就不起作用了（变成无穷大）。因此$m$的选择除了要满足上面误差控制的需求外，还要保证满桶的概率非常小。

上面已经说过，$u$满足二项分布，而当$n$非常大，$p$非常小时，可以用泊松分布近似逼近二项分布。因此这里我们可以认为$u$服从泊松分布（注意，上面我们说$u$也可以近似服从正态分布，这并不矛盾，实际上泊松分布和正态分布分别是二项分布的离散型和连续型概率逼近，且泊松分布以正态分布为极限）：

当$n、m$趋于无穷大时：

\begin{equation} Pr(u=k)=(\frac{\lambda^k}{k!})e^{-\lambda} \end{equation}

因此：

\begin{equation} Pr(u=0)<e^{-5}=0.007 \end{equation}

由于泊松分布的方差为$\lambda$，因此只要保证$u$的期望偏离$0$点$\sqrt{5}$的标准差就可以保证满桶的概率不大于$0.7%$。因此可得：

\begin{equation} m > 5(e^t-t-1) \end{equation}

NOTE:上式没看懂,望看懂的童鞋不吝赐教！

综上所述，当基数量级为$N$，可接受误差为$\epsilon$，则$m$的选取应该遵从

\begin{equation} m > \beta(e^t-t-1) \end{equation}

其中$\beta = max(5, 1/(\epsilon t)^2)$

下图是论文作者预先计算出的关于不同基数量级和误差情况下，$m$的选择表：

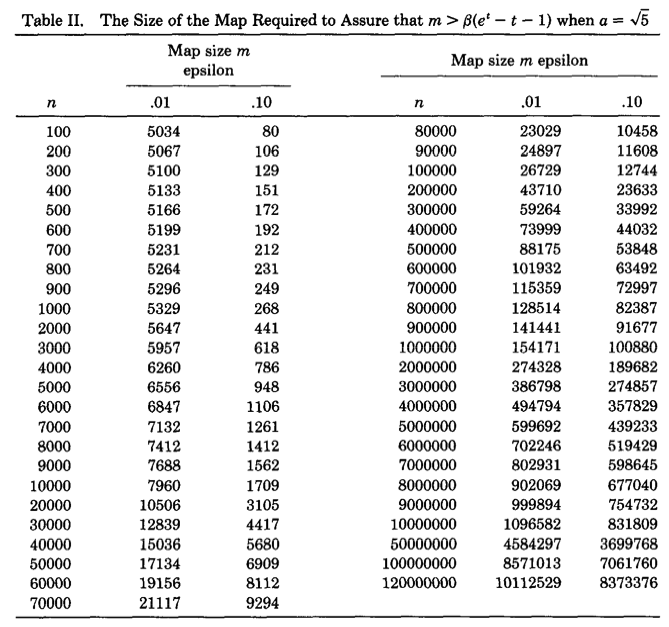
可以看出精度要求越高，则Bitmap的长度越大。随着$m$和$n$的增大，$m$大约为$n$的十分之一。因此LC所需要的空间只有传统的Bitmap直接映射方法的1/10，但是从渐进复杂性的角度看，空间复杂度仍为$O(N_{max})$。

合并

LC非常方便于合并，合并方案与传统Bitmap映射方法无异，都是通过按位或的方式。

LogLog Counting³

---

上一部分介绍的Linear Counting算法相较于直接映射Bitmap的方法能大大节省内存（大约只需后者1/10的内存），但毕竟只是一个常系数级的降低，空间复杂度仍然为$O(N_max)$。而本文要介绍的LogLog Counting却只有$O(log_2(log_2(N_{max})))$。例如，假设基数的上限为1亿，原始Bitmap方法需要12.5M内存，而LogLog Counting只需不到1K内存（640字节）就可以在标准误差不超过4%的精度下对基数进行估计，效果可谓十分惊人。

本部分将介绍LogLog Counting。

简介

LogLog Counting（以下简称LLC）出自论文“Loglog Counting of Large Cardinalities”。LLC的空间复杂度仅有$O(log_2(log_2(N_{max})))$，使得通过KB级内存估计数亿级别的基数成为可能，因此目前在处理大数据的基数计算问题时，所采用算法基本为LLC或其几个变种。下面来具体看一下这个算法。

基本算法

均匀随机化

与LC一样，在使用LLC之前需要选取一个哈希函数$H$应用于所有元素，然后对哈希值进行基数估计。$H$必须满足如下条件（定性的）：

• $H$的结果具有很好的均匀性，也就是说无论原始集合元素的值分布如何，其哈希结果的值几乎服从均匀分布（完全服从均匀分布是不可能的，D.Knuth已经证明不可能通过一个哈希函数将一组不服从均匀分布的数据映射为绝对均匀分布，但是很多哈希函数可以生成几乎服从均匀分布的结果，这里我们忽略这种理论上的差异，认为哈希结果就是服从均匀分布）。
• $H$的碰撞几乎可以忽略不计。也就是说我们认为对于不同的原始值，其哈希结果相同的概率非常小以至于可以忽略不计。
• $H$的哈希结果是固定长度的。

以上对哈希函数的要求是随机化和后续概率分析的基础。后面的分析均认为是针对哈希后的均匀分布数据进行。

思想来源

下面非正式的从直观角度描述LLC算法的思想来源。

设$a$为待估集合（哈希后）中的一个元素，由上面对$H$的定义可知，$a$可以看做一个长度固定的比特串（也就是$a$的二进制表示），设$H$哈希后的结果长度为$L$比特，我们将这$L$个比特位从左到右分别编号为$1、2、…、L$：

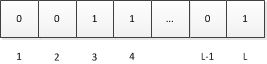
又因为$a$是从服从均与分布的样本空间中随机抽取的一个样本，因此$a$每个比特位服从如下分布且相互独立。

\begin{equation} P(x=k)=\left \lbrace \begin{array}{cc} 0.5 & (k=0) \\ 0.5 & (k=1) \end{array} \right. \end{equation}

通俗说就是$a$的每个比特位为0和1的概率各为0.5，且相互之间是独立的。

设$\rho(a)$为$a$的比特串中第一个“1”出现的位置，显然$1≤\rho(a)≤L$，这里我们忽略比特串全为0的情况（概率为$1/2^L$）。如果我们遍历集合中所有元素的比特串，取$\rho_{max}$为所有$\rho(a)$的最大值。

此时我们可以将$2^{\rho_{max}}$作为基数的一个粗糙估计，即：

\begin{equation} \hat{n} = 2^{\rho_{max}} \end{equation}

下面解释为什么可以这样估计。注意如下事实：

由于比特串每个比特都独立且服从0-1分布，因此从左到右扫描上述某个比特串寻找第一个“1”的过程从统计学角度看是一个伯努利过程，例如，可以等价看作不断投掷一个硬币（每次投掷正反面概率皆为0.5），直到得到一个正面的过程。在一次这样的过程中，投掷一次就得到正面的概率为$1/2$，投掷两次得到正面的概率是$1/2^2$，…，投掷k次才得到第一个正面的概率为$1/2^k$。

现在考虑如下两个问题：

1. 进行n次伯努利过程，所有投掷次数都不大于$k$的概率是多少？
2. 进行n次伯努利过程，至少有一次投掷次数等于$k$的概率是多少？

首先看第一个问题，在一次伯努利过程中，投掷次数大于$k$的概率为$1/2^k$，即连续掷出$k$个反面的概率。因此，在一次过程中投掷次数不大于$k$的概率为$1−1/2^k$。因此，$n$次伯努利过程投掷次数均不大于$k$的概率为：

\begin{equation} P_n(X \leq k)=(1-1/2^k)^n \end{equation}

显然第二个问题的答案是：

\begin{equation} P_n(X \neq k)=1-(1-1/2^{k-1})^n \end{equation}

从以上分析可以看出，当$n \ll 2^k$，$P_n(X \neq k)$的概率几乎为0，同时，当$n \gg k$时，$P_n(X \leq k)$的概率也几乎为0。用自然语言概括上述结论就是：当伯努利过程次数远远小于$2^k$时，至少有一次过程投掷次数等于$k$的概率几乎为0；当伯努利过程次数远远大于$2^k$时，没有一次过程投掷次数大于$k$的概率也几乎为0。

如果将上面描述做一个对应：一次伯努利过程对应一个元素的比特串，反面对应0，正面对应1，投掷次数$k$对应第一个“1”出现的位置，我们就得到了下面结论：

设一个集合的基数为$n$，$\rho_{max}$为所有元素中首个“1”的位置最大的那个元素的“1”的位置，如果$n$远远小于$2^{\rho_{max}}$，则我们得到$\rho_{max}$为当前值的概率几乎为0（它应该更小），同样的，如果$n$远远大于$2^{\rho_{max}}$，则我们得到$\rho_{max}$为当前值的概率也几乎为0（它应该更大），因此$2^{\rho_{max}}$可以作为基数$n$的一个粗糙估计。

分桶平均

上述分析给出了LLC的基本思想，不过如果直接使用上面的单一估计量进行基数估计会由于偶然性而存在较大误差。因此，LLC采用了分桶平均的思想来消减误差。具体来说，就是将哈希空间平均分成$m$份，每份称之为一个桶（bucket）。对于每一个元素，其哈希值的前$k$比特作为桶编号，其中$2^k=m$，而后$L-k$个比特作为真正用于基数估计的比特串。桶编号相同的元素被分配到同一个桶，在进行基数估计时，首先计算每个桶内元素最大的第一个“1”的位置，设为$M[i]$，然后对这$m$个值取平均后再进行估计，即：

\begin{equation} \hat{n}=2^{\frac{1}{m}\sum{M[i]}} \end{equation}

这相当于物理试验中经常使用的多次试验取平均的做法，可以有效消减因偶然性带来的误差。

下面举一个例子说明分桶平均怎么做。

假设$H$的哈希长度为16bit，分桶数$m$定为32。设一个元素哈希值的比特串为“0001001010001010”，由于$m$为32，因此前5个bit为桶编号，所以这个元素应该归入“00010”即2号桶（桶编号从0开始，最大编号为$m-1$），而剩下部分是“01010001010”且显然ρ(01010001010)=2，所以桶编号为“00010”的元素最大的$\rho$即为$M[2]$的值。

偏差修正

上述经过分桶平均后的估计量看似已经很不错了，不过通过数学分析可以知道这并不是基数n的无偏估计。因此需要修正成无偏估计。这部分的具体数学分析在“Loglog Counting of Large Cardinalities”中，过程过于艰涩这里不再具体详述，有兴趣的朋友可以参考原论文。这里只简要提一下分析框架：

首先上文已经得出：

\begin{equation} P_n(X \leq k)=(1-1/2^k)^n \end{equation}

因此：

\begin{equation} P_n(X = k)=(1-1/2^k)^n - (1-1/2^{k-1})^n \end{equation}

这是一个未知通项公式的递推数列，研究这种问题的常用方法是使用生成函数（generating function）。通过运用指数生成函数和poissonization得到上述估计量的Poisson期望和方差为：

\begin{equation} \begin{split} \varepsilon _n&\sim [(\Gamma (-1/m)\frac{1-2^{1/m}}{log2})^m+\epsilon _n]n \\ \nu _n&\sim [(\Gamma (-2/m)\frac{1-2^{2/m}}{log2})^m - (\Gamma (-1/m)\frac{1-2^{1/m}}{log2})^{2m}+\eta _n]n^2 \end{split} \end{equation}

其中$|\epsilon _n|$和$|\eta _n|$不超过$10^{−6}$。

最后通过depoissonization得到一个渐进无偏估计量：

\begin{equation} \hat{n}=\alpha _m 2^{\frac{1}{m}\sum{M[i]}} \end{equation}

其中：

其中$m$是分桶数。这就是LLC最终使用的估计量。

误差分析

不加证明给出如下结论：

\begin{equation} \begin{split} E_n(\hat{n})/n &= 1 + \theta_{1,n} + o(1) \\ \sqrt{Var_n(E)}/n &= \beta_m / \sqrt{m} + \theta_{2,n} + o(1) \end{split} \end{equation}

其中$|\theta_{1,n}|$和$|\theta_{2,n}|$不超过$10^{−6}$。

当$m$不太小（不小于64）时，$\beta$大约为1.30。因此：

\begin{equation} StdError(\hat{n}/n) \approx \frac{1.30}{\sqrt{m}} \end{equation}

算法应用

误差控制

在应用LLC时，主要需要考虑的是分桶数$m$，而这个$m$主要取决于误差。根据上面的误差分析，如果要将误差控制在$\epsilon$之内，则：

\begin{equation} m > (\frac{1.30}{\epsilon})^2 \end{equation}

内存使用分析

内存使用与$m$的大小及哈希值得长度（或说基数上限）有关。假设$H$的值为32bit，由于$\rho_{max} \leq 32$，因此每个桶需要5bit空间存储这个桶的$\rho_{max}$，$m$个桶就是$5 \times m/8$字节。例如基数上限为一亿（约227），当分桶数$m$为1024时，每个桶的基数上限约为227/210=217，而$log_2(log_2(217))=4.09$，因此每个桶需要5bit，需要字节数就是$5×1024/8=640$，误差为$1.30 / \sqrt{1024} = 0.040625$，也就是约为$4%$。

合并

与LC不同，LLC的合并是以桶为单位而不是bit为单位，由于LLC只需记录桶的$\rho_{max}$，因此合并时取相同桶编号数值最大者为合并后此桶的数值即可。

HyperLogLog Counting及Adaptive Counting⁴

---

在前一部分，我们了解了LogLog Counting。LLC算法的空间复杂度为$O(log_2(log_2(N_{max})))$，并且具有较高的精度，因此非常适合用于大数据场景的基数估计。不过LLC也有自己的问题，就是当基数不太大时，估计值的误差会比较大。这主要是因为当基数不太大时，可能存在一些空桶，这些空桶的$\rho_{max}$为0。由于LLC的估计值依赖于各桶$\rho_{max}$的几何平均数，而几何平均数对于特殊值（这里就是指0）非常敏感，因此当存在一些空桶时，LLC的估计效果就变得较差。

本部分将要介绍的HyperLogLog Counting及Adaptive Counting算法均是对LLC算法的改进，可以有效克服LLC对于较小基数估计效果差的缺点。

评价基数估计算法的精度

首先我们来分析一下LLC的问题。一般来说LLC最大问题在于当基数不太大时，估计效果比较差。上文说过，LLC的渐近标准误差为$1.30/\sqrt{m}$，看起来貌似只和分桶数$m$有关，那么为什么基数的大小也会导致效果变差呢？这就需要重点研究一下如何评价基数估计算法的精度，以及“渐近标准误差”的意义是什么。

标准误差

首先需要明确标准误差的意义。例如标准误差为0.02，到底表示什么意义。

标准误差是针对一个统计量（或估计量）而言。在分析基数估计算法的精度时，我们关心的统计量是$\hat{n}/n$。注意这个量分子分母均为一组抽样的统计量。下面正式描述一下这个问题。

设$S$是我们要估计基数的可重复有限集合。$S$中每个元素都是来自值服从均匀分布的样本空间的一个独立随机抽样样本。这个集合共有$C$个元素，但其基数不一定是$C$，因为其中可能存在重复元素。设$f_n$为定义在$S$上的函数：

\begin{equation} f_n(S)=CardinalityofS \end{equation}

同时定义$\hat{f_n}$也是定义在$S$上的函数：

\begin{equation} f_\hat{n}(S)=LogLog\;estimate\;value\;of\;S \end{equation}

我们想得到的第一个函数值，但是由于第一个函数值不好计算，所以我们计算同样集合的第二个函数值来作为第一个函数值得估计。因此最理想的情况是对于任意一个集合两个函数值是相等的，如果这样估计就是100%准确了。不过显然没有这么好的事，因此我们退而求其次，只希望fn^(S)是一个无偏估计，即：

\begin{equation} f_\hat{n}(S) \end{equation}

这个在上一篇文章中已经说明了。同时也可以看到，$\frac{f_\hat{n}(S)}{f_n(S)}$实际上是一个随机变量，并且服从正态分布。对于正态分布随机变量，一般可以通过标准差$\sigma$度量其稳定性，直观来看，标准差越小，则整体分布越趋近于均值，所以估计效果就越好。这是定性的，那么定量来看标准误差$\sigma$到底表达了什么意思呢。它的意义是这样的：

对于无偏正态分布而言，随机变量的一次随机取值落在均值一个标准差范围内的概率是68.2%，而落在两个和三个标准差范围内的概率分别为95.4%和99.6%，如下图所示（图片来自维基百科）：

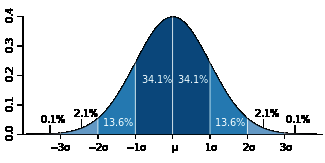
因此，假设标准误差是0.02（2%），它实际的意义是：假设真实基数为$n$，$n$与估计值之比落入(0.98, 1.02)的概率是68.2%，落入(0.96,1.04)的概率是95.4%，落入(0.94,1.06)的概率是99.6%。显然这个比值越大则估计值越不准，因此对于0.02的标准误差，这个比值大于1.06或小于0.94的概率不到0.004。

再直观一点，假设真实基数为10000，则一次估计值有99.6%的可能不大于10600且不小于9400。

组合计数与渐近分析

如果LLC能够做到绝对服从$1.30/\sqrt{m}$，那么也算很好了，因为我们只要通过控制分桶数$m$就可以得到一个一致的标准误差。这里的一致是指标准误差与基数无关。不幸的是并不是这样，上面已经说过，这是一个“渐近”标注误差。下面解释一下什么叫渐近。

在计算数学中，有一个非常有用的分支就是组合计数。组合计数简单来说就是分析自然数的组合函数随着自然数的增长而增长的量级。可能很多人已经意识到这个听起来很像算法复杂度分析。没错，算法复杂度分析就是组合计数在算法领域的应用。

举个例子，设$A$是一个有$n$个元素的集合（这里$A$是严格的集合，不存在重复元素），则$A$的幂集（即由$A$的所有子集组成的集合）有$2^n$个元素。

上述关于幂集的组合计数是一个非常整齐一致的组合计数，也就是不管$n$多大，A的幂集总有$2^n$个元素。

可惜的是现实中一般的组合计数都不存在如此干净一致的解。LLC的偏差和标准差其实都是组合函数，但是论文中已经分析出，LLC的偏差和标准差都是渐近组合计数，也就是说，随着$n$趋向于无穷大，标准差趋向于$1.30/\sqrt{m}$，而不是说$n$多大时其值都一致为$1.30/\sqrt{m}$。另外，其无偏性也是渐近的，只有当$n$远远大于$m$时，其估计值才近似无偏。因此当$n$不太大时，LLC的效果并不好。

庆幸的是，同样通过统计分析方法，我们可以得到$n$具体小到什么程度我们就不可忍受了，另外就是当$n$太小时可不可以用别的估计方法替代LLC来弥补LLC这个缺陷。HyperLogLog Counting及Adaptive Counting都是基于这个思想实现的。

Adaptive Counting

Adaptive Counting（简称AC）在“Fast and accurate traffic matrix measurement using adaptive cardinality counting”一文中被提出。其思想也非常简单直观：实际上AC只是简单将LC和LLC组合使用，根据基数量级决定是使用LC还是LLC。具体是通过分析两者的标准差，给出一个阈值，根据阈值选择使用哪种估计。

基本算法

如果分析一下LC和LLC的存储结构，可以发现两者是兼容的，区别仅仅在于LLC关心每个桶的$\rho_{max}$，而LC仅关心此桶是否为空。因此只要简单认为$\rho_{max}$值不为0的桶为非空，桶为空就可以使用LLC的数据结构做LC估计了。

而我们已经知道，LC在基数不太大时效果好，基数太大时会失效；LLC恰好相反，因此两者有很好的互补性。

回顾一下，LC的标准误差为：

\begin{equation} SE_{lc}(\hat{n}/n)=\sqrt{e^t-t-1}/(t\sqrt{m}) \end{equation}

LLC的标准误差为：

\begin{equation} SE_{llc}(\hat{n}/n)=1.30/\sqrt{m} \end{equation}

将两个公式联立：

\begin{equation} \sqrt{e^t-t-1}/(t\sqrt{m})=1.30/\sqrt{m} \end{equation}

解得$t \approx 2.89$。注意$m$被消掉了，说明这个阈值与$m$无关。其中$t=n/m$。

设$\beta$为空桶率，根据LC的估算公式，带入上式可得：

\begin{equation} \beta = e^{-t} \approx 0.051 \end{equation}

因此可以知道，当空桶率大于0.051时，LC的标准误差较小，而当小于0.051时，LLC的标准误差较小。 完整的AC算法如下：

\begin{equation} \hat{n}=\left \lbrace \begin{array}{cc} \alpha_m m2^{\frac{1}{m}\sum{M}} & if & 0 \leq \beta < 0.051 \\ -mlog(\beta) & if & 0.051 \leq \beta \leq 1 \end{array} \right. \end{equation}

误差分析

因为AC只是LC和LLC的简单组合，所以误差分析可以依照LC和LLC进行。值得注意的是，当β<0.051时，LLC最大的偏差不超过0.17%，因此可以近似认为是无偏的。

HyperLogLog Counting

HyperLogLog Counting（以下简称HLLC）的基本思想也是在LLC的基础上做改进，不过相对于AC来说改进的比较多，所以相对也要复杂一些。本文不做具体细节分析，具体细节请参考“HyperLogLog: the analysis of a near-optimal cardinality estimation algorithm”这篇论文。

基本算法

HLLC的第一个改进是使用调和平均数替代几何平均数。注意LLC是对各个桶取算数平均数，而算数平均数最终被应用到2的指数上，所以总体来看LLC取得是几何平均数。由于几何平均数对于离群值（例如这里的0）特别敏感，因此当存在离群值时，LLC的偏差就会很大，这也从另一个角度解释了为什么n不太大时LLC的效果不太好。这是因为n较小时，可能存在较多空桶，而这些特殊的离群值强烈干扰了几何平均数的稳定性。

因此，HLLC使用调和平均数来代替几何平均数，调和平均数的定义如下：

\begin{equation} H = \frac{n}{\frac{1}{x_1} + \frac{1}{x_2} + ... + \frac{1}{x_n}} = \frac{n}{\sum_{i=1}^n \frac{1}{x_i}} \end{equation}

调和平均数可以有效抵抗离群值的扰动。使用调和平均数代替几何平均数后，估计公式变为如下：

\begin{equation} \hat{n}=\frac{\alpha_m m^2}{\sum{2^{-M}}} \end{equation}

其中：

\begin{equation} \alpha_m=(m\int _0^\infty (log_2(\frac{2+u}{1+u}))^m du)^{-1} \end{equation}

偏差分析

根据论文中的分析结论，与LLC一样HLLC是渐近无偏估计，且其渐近标准差为：

\begin{equation} SE_{hllc}(\hat{n}/n)=1.04/\sqrt{m} \end{equation}

因此在存储空间相同的情况下，HLLC比LLC具有更高的精度。例如，对于分桶数$m$为$2^13$（8k字节）时，LLC的标准误差为1.4%，而HLLC为1.1%。

分段偏差修正

在HLLC的论文中，作者在实现建议部分还给出了在$n$相对于$m$较小或较大时的偏差修正方案。具体来说，设$E$为估计值：

当$E≤{5 \over 2}m$时，使用LC进行估计。

当$\frac{5}{2}m < E \leq \frac{1}{30}2^{32}$时，使用上面给出的HLLC公式进行估计。

当$E>\frac{1}{30}2^{32}$时，估计公式则为$\hat{n}=-2^{32}log(1-E/2^{32})$。

关于分段偏差修正效果分析也可以在原论文中找到。

写在后面

---

原博客中作者对这几种算法进行了实验比较,因为个人对实验不是很感兴趣,现只摘录作者的个人建议(对实验结果有兴趣的同学请参考五种常用基数估计算法效果实验及实践建议):

• Linear Counting和LogLog Counting由于分别在基数较大和基数较小（阈值可解析分析，具体方法和公式请参考后文列出的相关论文）时存在严重的失效，因此不适合在实际中单独使用。一种例外是，如果对节省存储空间要求不强烈，不要求空间复杂度为常数（Linear Counting的空间复杂度为$O(n)$，其它算法均为$O(1)$），则在保证Bitmap全满概率很小的条件下，Linear Counting的效果要优于其它算法。
• 总体来看，不论哪种算法，提高分桶数都可以降低偏差和方差，因此总体来看基数估计算法中分桶数的选择是最重要的一个权衡——在精度和存储空间间的权衡。
• 实际中，Adaptive Counting或HyperLogLog Counting都是不错的选择，前者偏差较小，后者对离群点容忍性更好，方差较小。
• Google的HyperLogLog Counting++算法属于实验性改进，缺乏严格的数学分析基础，通用性存疑，不宜在实际中贸然使用。

最后感谢CodingLabs撰写的精彩博文,这两周就写这3篇博文吧，两周后再见。尼玛,都2:16了,大家晚安，睡了。

1. 解读Cardinality Estimation算法（第一部分：基本概念） ↩
2. 解读Cardinality Estimation算法（第二部分：Linear Counting） ↩
3. 解读Cardinality Estimation算法（第三部分：LogLog Counting） ↩
4. 解读Cardinality Estimation算法（第四部分：HyperLogLog Counting及Adaptive Counting） ↩

---