苹果的味道

小小收藏夹(I)

五 06 六月 2014

Filed under Pearls

Tags 算法 Fun Staff 收藏夹 Bloom Filter B Trees Data Structure Algorithm PGM

傅里叶变换及应用(上)

本部分为傅里叶变换及应用(上),由于本文篇幅已经比较长了,所以将傅立叶变换及应用(下)及以后收藏的内容搬至小小收藏夹(II),特此说明。

  • 周期性，三角函数表示复杂函数;分析了一个周期，多个频率的经典概念，给出了傅里叶级数的指数表示形式,本视频中假定该等式成立，推导出每一分量需要满足的数学形式。本视频的内容个人总结为以下图片:

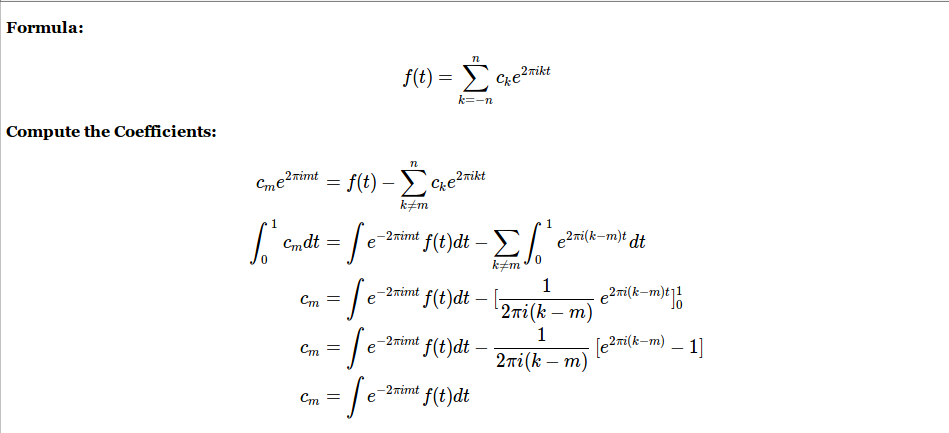
Fourier Coefficients

Convergence in mean(Convergence in energy):

假定$f(t)$是周期函数，且$\int_0^1 |f(t)|^2 dt < \infty$,那么该函数可表示为傅里叶级数的形式，且有: 当$n \to \infty$时，我们有: \begin{equation} \int_0^1 |\sum_{k=-n}^n c_ke^{2\pi ikt}-f(t)|^2 dt \to 0 \end{equation}

  • 傅里叶级数;好吧,就不写简介了,我只想说这个老师真的很有趣，很幽默，不服去看(还有,数学真的很优美，不服就多学点数学吧)。

如果函数$f$和$g$是平方可积的(它们均可以是复数函数),即$f,g \in L^2[0,1]$,那么函数之间的内积可定义为:

\begin{equation} (f,g) = \int_0^1 f(t)\bar{g(t)}dt \end{equation}

若上式为0,我们则说$f,g$是正交的。 另，我们定义函数的长度或模为:

\begin{equation} ||f||^2 = (f,f) = \int_0^1 |f(t)|^2 dt \end{equation}

接下来,根据Rayleigh's Equality,我们有:

\begin{equation} \int_0^1 |f(t)|^2 dt = \sum_{k=-n}^n |c_k|^2 \end{equation}

  • 傅里叶级数连续性讨论，热方程;本集通过对于热方程的推导引出了卷积的概念；另，教授试图通过使周期趋近于无穷的方法使得原来适用于周期函数的内容可以拓展到非周期函数上，可是这种情况下会出现傅里叶系数趋近于0的情况，怎么办呢?请看下集。小小地总结一下:

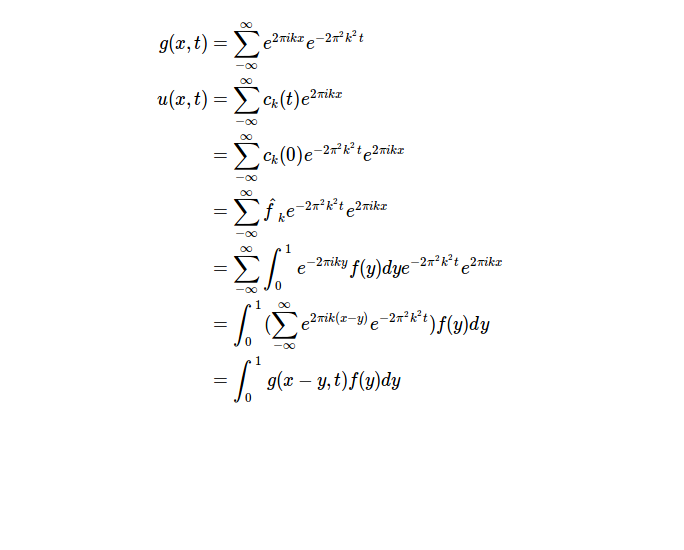
intro_convolution

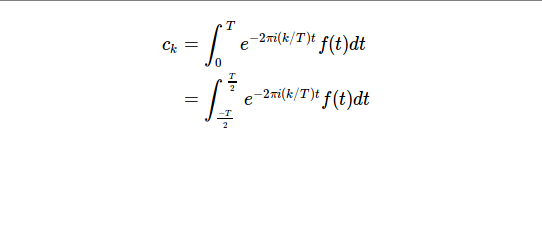
non_periodic_fourier_coefficients

  • 热方程讨论;本视频中我们成功从傅立叶级数扩展到了傅立叶变换。视频中给出了矩形函数以及三角函数的傅立叶展开式,it's quite amazing.同样，还是总结一下:

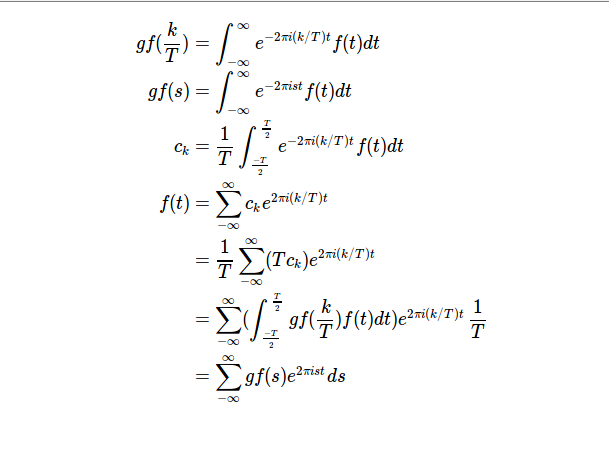
Fourier Transform

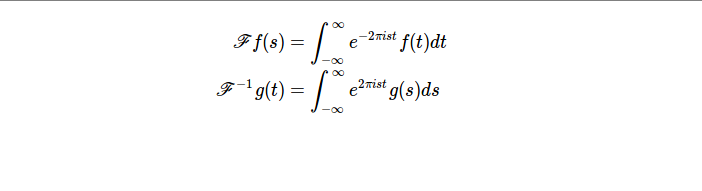
Fourier_Transform_Inverse

  • 傅里叶正（反）变换复习;

    • 对于形如$f(t)=e^{-\pi t^2}$的归一化后的高斯函数而言，我们有:

    \begin{equation} \int_{-\infty}^{\infty} f(t)dt =1 \end{equation}

    • 高斯函数的傅立叶变化是其自身。

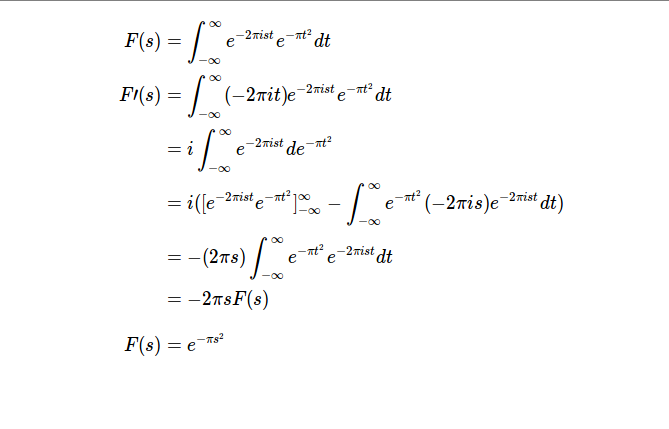
    Fourier_Transform_Gaussian

    • 对偶性Duality;

    \begin{equation} \begin{split} \mathscr{F} f(-s) &= \int_{-\infty}^{\infty} e^{-2\pi i(-s)t} f(t)dt \\ &= \int_{-\infty}^{\infty} e^{2\pi ist}f(t)dt \\ &= \mathscr{F}^{-1} f(s) \\ \mathscr{F}(f^-) &= \mathscr{F}^{-1} f = (\mathscr{F}f)^- \end{split} \end{equation}

Pocket

Computer Vision

  • 特征检测与匹配;一个由浅入深、逐渐深入的介绍特征检测与匹配方法的灰常好的一个Slides.
  • 人脸识别算法初次了解;初步介绍了一些人脸识别的基本知识及部分相关算法，可作为人脸识别的入门材料。

TOOLS

NLP1

  • Relation Extraction
    • Hand-written approach more suitable for structured data,such as a telephone book,Facebook or eBay;
    • Supervised Method;得到所有的命名实体组,使用一个分类器(features)判断它们是否是关联的,如果是,则使用第二个分类器判断它们之间的关联关系具体是什么;
    • Semi-Supervised(Relation Bootstrapping/Distant Supervised Learning) and unsupervised methods(Open Information Extraction);Strapping方法感觉很巧妙,个人很喜欢;

SVM

对于SVM这么高端大气上档次的东西,当然要单独列出来。今天其他东西实在看不下去了,所以把Pluskid之前写的一系列讲SVM的文章再挖出来看看。以下是目录以及对每篇的简单说明:

  • 支持向量机: Maximum Margin Classifier;文中主要介绍了两个距离,Functional Margin $\hat{\gamma}$和Geometrical Margin $\tilde{\gamma}$.它们之间满足$\hat{\gamma} = ||w||\tilde{\gamma}$.我们固定$\hat{\gamma} = 1$,通过最大化$\frac{1}{||w||}$来得到Maximum Margin Classifier.
  • 支持向量机: Support Vector;简要介绍了Support Vector是指什么,另外对线性可分的情况利用Duality进行了推导并得出了两个比较重要的结论:
    • 对新点的预测只需要计算与训练点之间的内积即可;
    • 非支持向量不参与模型的计算过程之中。
  • 支持向量机: Kernel;Kernel的基本思想。
  • 支持向量机：Outliers;通过引入松弛变量处理Outliers,而实际上最后的优化形式只是加上$\alpha_i \leq C$的限制。
  • 支持向量机：Numerical Optimization;以非常通俗易懂的方式介绍了一下SMO(Sequential Minimal Optimization),赞一个。

Deep Learning

  • 稀疏编码(Sparse Coding)

Deep Learning（深度学习）学习笔记整理系列之（五)

  • Deep Learning总结

Deep Learning（深度学习）学习笔记整理系列之（八)

  • 受限Boltzmann机

A Brief Introduction to Restricted Boltzmann Machine

算法

  • 今天看了一下网上流传的传说中的高大上的所谓的十大海量数据处理算法,看了一下,实际上没有什么东西,唯独Bloom Filter看着还挺好玩的,所以以下给出一个通俗易懂的链接。

那些优雅的数据结构(1) : BloomFilter——大规模数据处理利器

  • 在过去的若干年里,有一个心结一直萦绕在我的心头挥之不去,它存在于我的脑海里，我的梦里，我的歌声里,TA就是B树(好吧,其实是因为没有机会好好地研究一下它啦)。以下给出两个链接,它们主要介绍了B树的基本概念,性质以及针对B树的插入、删除操作,两个PPT还是相当直观的,应该能够比较直观地了解B树这个数据结构!

  • 今天又重新看了一下这个写的很不错的A*算法,恩,这篇文章想来是极好的。

A星寻路算法介绍

  • 复习一下之前做智能提示时用到的Trie Tree.

Indexed Search Tree (Trie) - Computer Science Department

  • 看了一下传说中的数据挖掘十大算法,好像就Apriori算法不是特别熟吧,所以重新看了一遍;个人觉得如果我早出生若干年,这种程度的算法也是能想出来的吧(我指思想).好吧,我认为着重要理解的有如下两点:
    • Support;其实也就是某种组合在所有Transaction中出现的频度。
    • Confidence;当生成关联规则$A\to B$时,有$confidence = \frac{Count(A,B)}{Count(A)}$,背后的Intuition就是如果我买了$A$,大概会有多大的可能买$B$.

Apriori Algorithm Review for Finals

  • 最近需要对1G的文本数据进行处理,所以想了解一下现行的分布式计算框架的应用场景,从而选择合适的框架用于这个任务,期间看到以下两篇文章写的很不错,特此摘录。

对实时分析与离线分析的思考 对实时分析与离线分析的思考(二)

  • 最近脑子总是不断宕机,宕机了就什么也看不了了,刚看了一篇一个人讲自己怎么学习算法的博文,感觉还不错(只是看了作者的经历,他看过的那些书还没来得及看)。以下给出链接:

我的算法学习之路

Machine Learning

  • 看的有点累了,不想看EM算法复杂的数学公式推导了,所以找到之前看过的一篇,回顾一下,等以后想看了再详细介绍Mixture Models和EM算法吧!

漫谈 Clustering (3): Gaussian Mixture Model

  • 近期为了理解卷积,于是到处找资料,无意中发现了这一篇神一般的理解。(墙裂推荐)

关于卷积的一个血腥的讲解，看完给跪了

  • PCA数据预处理Whitening

在使用PCA前需要对数据进行预处理，首先是均值化，即对每个特征维，都减掉该维的平均值，然后就是将不同维的数据范围归一化到同一范围，方法一般都是除以最大值。但是比较奇怪的是，在对自然图像进行均值处理时并不是不是减去该维的平均值，而是减去这张图片本身的平均值。因为PCA的预处理是按照不同应用场合来定的。

自然图像指的是人眼经常看见的图像，其符合某些统计特征。一般实际过程中，只要是拿正常相机拍的，没有加入很多人工创作进去的图片都可以叫做是自然图片，因为很多算法对这些图片的输入类型还是比较鲁棒的。在对自然图像进行学习时，其实不需要太关注对图像做方差归一化，因为自然图像每一部分的统计特征都相似，只需做均值为0化就ok了。不过对其它的图片进行训练时，比如首先字识别等，就需要进行方差归一化了。

有一个观点需要注意，那就是PCA并不能阻止过拟合现象。表明上看PCA是降维了，因为在同样多的训练样本数据下，其特征数变少了，应该是更不容易产生过拟合现象。但是在实际操作过程中，这个方法阻止过拟合现象效果很小，主要还是通过规则项来进行阻止过拟合的。

Whitening：

Whitening的目的是去掉数据之间的相关联度，是很多算法进行预处理的步骤。比如说当训练图片数据时，由于图片中相邻像素值有一定的关联，所以很多信息是冗余的。这时候去相关的操作就可以采用白化操作。数据的Whitening必须满足两个条件：

  • 不同特征间相关性最小，接近0；
  • 所有特征的方差相等（不一定为1）。

常见的白化操作有PCA whitening和ZCA whitening。

PCA whitening是指将数据x经过PCA降维为z后，可以看出z中每一维是独立的，满足whitening白化的第一个条件，这是只需要将z中的每一维都除以标准差就得到了每一维的方差为1，也就是说方差相等。公式为：

\begin{equation} x_{PCAwhite,i} = \frac{x_{rot,i}}{\sqrt{\lambda_i}} \end{equation}

ZCA whitening是指数据x先经过PCA变换为z，但是并不降维，因为这里是把所有的成分都选进去了。这是也同样满足whtienning的第一个条件，特征间相互独立。然后同样进行方差为1的操作，最后将得到的矩阵左乘一个特征向量矩阵U即可。ZCA whitening公式为：

\begin{equation} x_{ZCAwhite} = Ux_{PCAwhite} \end{equation}

参考Deep learning：十(PCA和whitening)

  • 最近一直在看高斯过程,挺难理解的,好吧,咱们慢慢来,先给个链接。

Introduction to Gaussian Process * 今天看自然语言处理Standford公开课的时候看到最大熵模型(Maximum Entropy Models),视频讲的实在太罗嗦了,在网上找了找,下面这个PPT貌似还挺不错的。(原始PPT有部分错误,以下网盘共享文件是部分修正后版本,可能还会有错误,欢迎指出)

Maximum Entropy Model

  • EM/pLSA/LDA的一些参考资料

    • Christopher M. Bishop. Pattern Recognition and Machine Learning (Information Science and Statistics). Springer-Verlag New York, Inc., Secaucus, NJ, USA, 2006.
    • Gregor Heinrich. Parameter estimation for text analysis. Technical report, 2004.
    • Wayne Xin Zhao, Note for pLSA and LDA, Technical report, 2011.
    • CX Zhai, A note on the expectation-maximization (em) algorithm 2007
    • Qiaozhu Mei, A Note on EM Algorithm for Probabilistic Latent Semantic Analysis 2008
    • Christopher D. Manning, Prabhakar Raghavan and Hinrich Schütze, Introduction to Information Retrieval, Cambridge University Press. 2008.
    • Freddy Chong Tat Chua. Dimensionality reduction and clustering of text documents.Technical report, 2009.

  • LDA算法伪代码实现参考

  • A Very Brief Introduction about Semi-supervised Learning.

SEMI_SUPERVISED LEARNING

PGM

以下给出讲解PGM比较深入浅出的一系列Lecture Slides。

PART I:Introduction to PGM

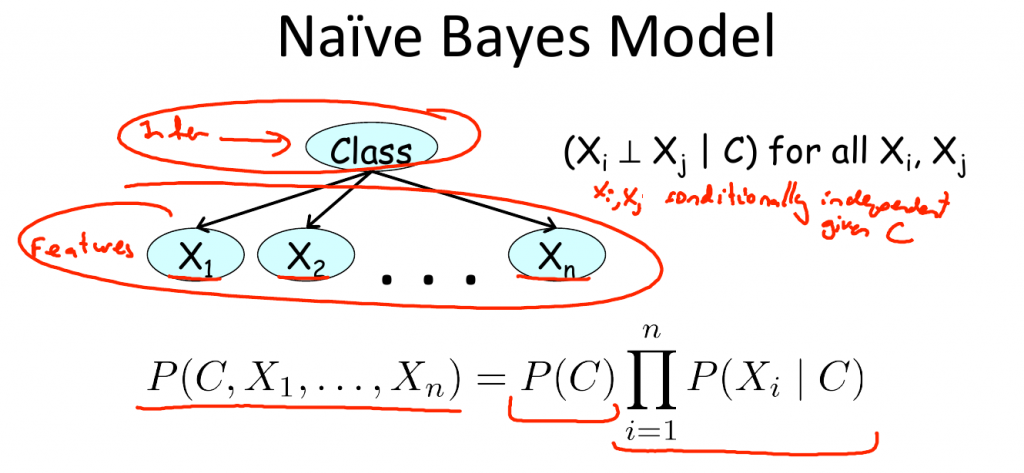
Naive Bayes Classifier

  • Template Models;主要介绍了Template Models,包括Bayesian Network(HMM)以及Plate Models;
  • Structured CPDs;介绍了几种CPD表示的其他常见形式,包括:
    • Deterministic CPDs
    • Tree-structured CPDs
    • Logistic CPDs & generalizations
    • Noisy OR/AND
    • Linear Gaussian & generalizations
  • Markov Network Fundamentals;本部分涵盖的内容有Markov Network,General Gibbs Distribution,CRF,Log-Linear Models.(Logistic Models is a simple CRF;CRF does not need to concern about the correlation between features!)

PART II:PGM Inference

  • Variable Elimination;简要介绍了如何在Bayesian Network以及Ｍarkov Network中执行VE算法;接着对其复杂度进行了分析;最后从图的视角重新审视了一下VE算法.

Variable Elimination

  • Belief Propagation(I) & Belief Propagation(II);其基本内容如下:
    • Belief Propagation算法基本流程;
    • Cluster Graph的基本性质(BP does poorly when we have strong correlations!);
    • BP算法的基本性质;
    • Clique Tree Algorithm.

Belief Propagation

PART III:PGM Learning

NOTE:该课程网址见PGM.

TODO Board:

  • Ising Model
  • Dual Decomposition
  • Decision Making
  • Bayesian Scores
  • Learning With Incomplete Data
  • Lassos
  • 凸QP
  • Duality
  • KKT条件
  • 支持向量机番外篇I:支持向量机：Duality
  • 支持向量机番外篇II:支持向量机：Kernel II
  • Apriori算法细节
  • pLSA算法EM算法求解
  1. Natural Language Processing ↩

Comments

苹果的味道 © qingyuanxingsi Powered by Pelican and Twitter Bootstrap. Icons by Font Awesome and Font Awesome More