Clustering和Classification无疑是机器学习领域两个重量级的TASK,而且这两个概念作为初学者是比较容易混淆的。以下简要说明一下这两个概念之间的区别。Classification和Clustering都是要把一堆Objects分到不同的Group,但是两者还是有很明显的差异的。具体而言,Classification属于Supervised Learning,即训练样本必须是已标注样本,而聚类是Unsupervised Learning,我们要从未标注样本中进行学习,然后把Objects分到不同的Group中去。
言归正传,Clustering,一言以蔽之,其核心思想就是"物以类聚,人以群分"。但是其核心前提在于物以何聚,人以何分,即使用什么用来度量Objects之间的差异性。一种比较自然的想法就是使用Objects属性之间的差异用以度量Objects之间的差异性。
\begin{equation} \Delta(x_i,x_{x\prime}) = \sum_{j=1}^D \Delta_j(x_{ij},x_{x\prime j}) \end{equation}
常见的用来Capture属性之间差异性的函数则有如下几种:
- 高斯距离
大家最熟悉的无疑就是高斯距离了,当然,其只能应用于实数值。
\begin{equation} \Delta_j (x_{ij},x_{x\prime j}) = (x_{ij}-x{i\prime j})^2 \end{equation}
- 街区距离($l_1$距离)
高斯距离由于采用二次形式,因此较大的差异容易被放大化,因此在很多场景下Gaussian距离对于Outliers很敏感。为了解决这个问题,人们引入了街区距离(city block distance),直观上理解就是在一个街区中我们从一点到另外一点要经过的街区数。定义如下:
\begin{equation} \Delta_j (x_{ij},x_{x\prime j}) = |x_{ij}-x_{i\prime j}| \end{equation}
- 海明距离
对于类别类型的变量,如{red,green,blue},我们通常采用的办法则是当特征不同时,赋值为1,否则赋值为0;将所有的类别型变量相加有:
\begin{equation} \Delta(x_i,x_{i\prime}) = \sum_{j=1}^D 1_{x_{ij} \neq x_{x\prime j}} \end{equation}
有了衡量Objects之间差异性的尺度,我们就能采用合适的算法将Objects分到不同的Group当中去。在正式介绍相关算法之间,我们还是简要说明一下如何衡量不同的聚类方法的好坏。
聚类方法评价
总体而言,聚类算法的核心目的即在于将相似的Objects分到同一类中去,并保证不同类之间的Objects之间的差异性。目前针对聚类算法广泛使用的评价指标有如下三种:
Purity
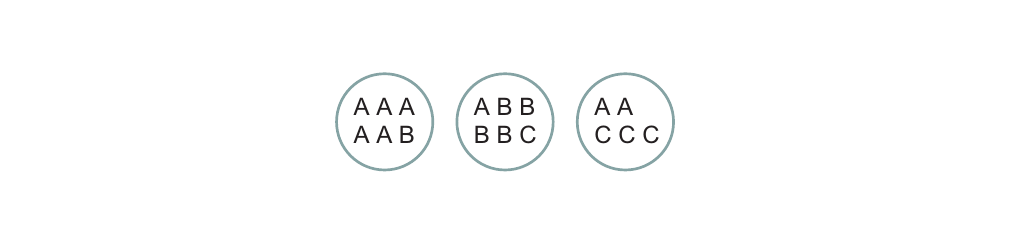
如上图所示,每一个圆圈代表一个Cluster,每个圆圈内的物体均已被标注为{A,B,C}中的一种。令$N_{ij}$表示Cluster i中label为j的物体的数目,$N_i$表示Cluster i中物体的总数。另一个cluster的纯度(purity)被定义为$p_i \triangleq max_j p_{ij}$,因此整个聚类结果的纯度为:
\begin{equation} purity \triangleq \sum_{i} \frac{N_i}{N}p_i \end{equation}
根据上述定义,上图中聚类结果的纯度为:
${6 \over 17}{5 \over 6}+{6 \over 17}{4 \over 6}+{5 \over 17}{3 \over 5} = 0.71$
不难看出,聚类的纯度越高,则表明该聚类算法越好。
Rand index
令$U={u_1,...,u_R}$和$V={v_1,...,v_C}$分别表示对于$N$个数据点的两种不同的划分方式。例如,$U$可能是我们估计的聚类结果,而$V$则是根据物体的Label得到的参考聚类结果。现我们定义如下四个值:
- TP(True Positives):同时属于$U$和$V$中同一集合的物体对的数目,即不管对于$U$还是$V$而言,这些物体对均被分配到同一集合中;
- TN(True Negatives):对于$U$和$V$而言,被分配到不同集合的物体对的数目,即在参考聚类中,它们被分到不同的集合,在我们估计的聚类结果中,它们也被划分到不同的集合。
- FP(False Positives):在$V$中被分配到不同集合,而在$U$中被分配到相同集合的物体对的数目。
- FN(False Negatives):在$V$中被分配到相同集合,而在$U$中被分配到不同集合的物体对的数目。
而Rand index被定义为:
\begin{equation} R \triangleq \frac{TP+TN}{TP+FP+FN+TN} \end{equation}
即我们估计的结果中被分配到正确的类中的物体对所占的比例。显然,$0 \leq R \leq 1$.
还是举上图中的例子为例,说明其计算过程:
上图中三个Cluster中点的个数分别是6,6,5.因此其中“positives”的数目为:
\begin{equation} TP+FP = C_6^2+C_6^2+C_5^2 = 40 \end{equation}
其中True Positives的数目为:
\begin{equation} TP = C_5^2+C_4^2+C_2^2+C_3^2 = 20 \end{equation}
同理我们可以得到$FN=24,TN=72$.因此我们有$R = \frac{20+72}{40+24+72} = 0.68$.
Mutual Information
另外一种衡量聚类质量的方法是计算$U$和$V$之间的互信息。关于互信息的内容请参考机器学习系列(II):Generative models for discrete data,此处不再赘述。
基本聚类算法
本部分会着重介绍三种聚类算法,包括K-means,Spectral Clustering以及Hierarchical Clustering,且容我一一道来。
K-Means & K-Medoids
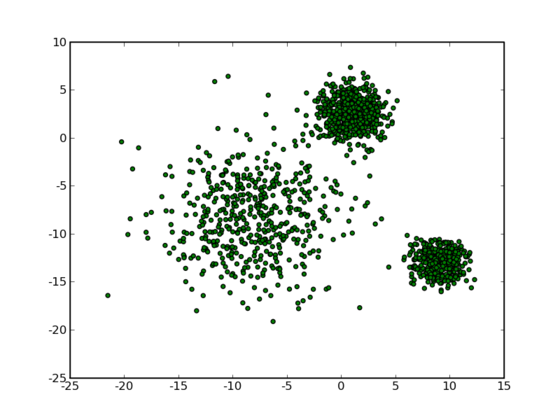
如上图所示,对于二维空间上的若干个点,我们要将它们分成若干类。我们直观上来看,上图中数据点大致可以分为3类,如果我们将每一类用不同的颜色标注,则可得到下图:
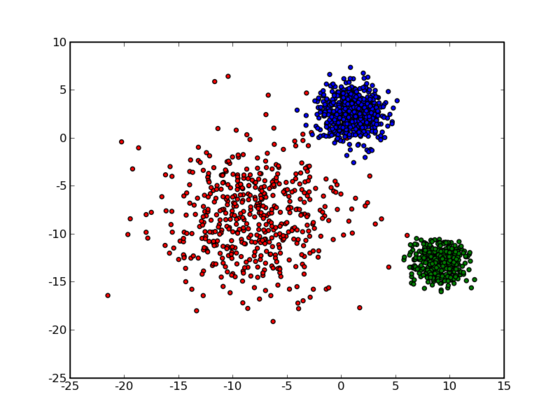
那么计算机要如何来完成这个任务呢?当然,计算机还没有高级到能够“通过形状大致看出来”,不过,对于这样的$N$维欧氏空间中的点进行聚类,有一个非常简单的经典算法,也就是本节我们要介绍的K-Means。在介绍K-Means的具体步骤之前,让我们先来看看它对于需要进行聚类的数据的一个基本假设吧:对于每一个cluster,我们可以选出一个中心点(center),使得该cluster中的所有的点到该中心点的距离小于到其他cluster的中心的距离。虽然实际情况中得到的数据并不能保证总是满足这样的约束,但这通常已经是我们所能达到的最好的结果,而那些误差通常是固有存在的或者问题本身的不可分性造成的。例如下图所示的两个高斯分布,从两个分布中随机地抽取一些数据点出来,混杂到一起,现在要让你将这些混杂在一起的数据点按照它们被生成的那个分布分开来:
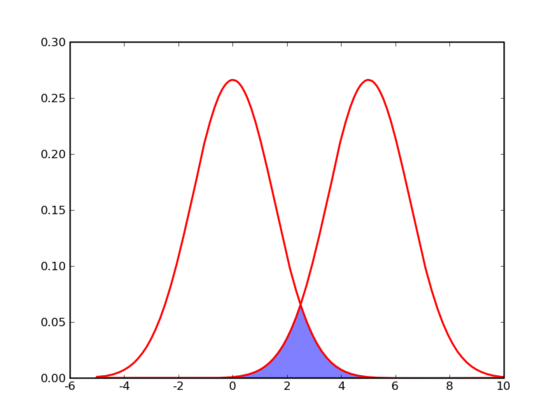
由于这两个分布本身有很大一部分重叠在一起了,例如,对于数据点2.5来说,它由两个分布产生的概率都是相等的,你所做的只能是一个猜测;稍微好一点的情况是2,通常我们会将它归类为左边的那个分布,因为概率大一些,然而此时它由右边的分布生成的概率仍然是比较大的,我们仍然有不小的几率会猜错。而整个阴影部分是我们所能达到的最小的猜错的概率,这来自于问题本身的不可分性,无法避免。因此,我们将K-Means所依赖的这个假设看作是合理的。
基于这样一个假设,我们再来导出K-Means所要优化的目标函数:设我们一共有$N$个数据点需要分为$K$个cluster,K-Means要做的就是最小化:
\begin{equation} J = \sum_{n=1}^N\sum_{k=1}^K r_{nk} \|x_n-\mu_k\|^2 \end{equation}
其中$r_{nk}$在数据点$n$被归类到cluster k的时候为1,否则为0。直接寻找$r_{nk}$和$\mu_k$来最小化$J$并不容易,不过我们可以采取迭代的办法:先固定$\mu_k$,选择最优的$r_{nk}$,很容易看出,只要将数据点归类到离他最近的那个中心就能保证J最小。下一步则固定$r_{nk}$,再求最优的$\mu_k$。将$J$对$\mu_k$ 求导并令导数等于零,很容易得到$J$最小的时候$\mu_k$应该满足:
\begin{equation} \mu_k=\frac{\sum_n r_{nk}x_n}{\sum_n r_{nk}} \end{equation} 亦即$\mu_k$的值应当是所有cluster k中的数据点的平均值。由于每一次迭代都是取到$J$的最小值,因此$J$只会不断地减小(或者不变),而不会增加,这保证了K-Means最终会到达一个极小值。虽然K-Means并不能保证总是能得到全局最优解,但是对于这样的问题,像K-Means这种复杂度的算法,这样的结果已经是很不错的了。
下面我们来总结一下K-Means算法的具体步骤:
- 选定$K$个中心$\mu_k$的初值。这个过程通常是针对具体的问题有一些启发式的选取方法,或者大多数情况下采用随机选取的办法。因为前面说过K-Means并不能保证全局最优,而是否能收敛到全局最优解其实和初值的选取有很大的关系,所以有时候我们会多次选取初值跑K-Means,并取其中最好的一次结果。
- 将每个数据点归类到离它最近的那个中心点所代表的cluster中。
- 用公式$\mu_k = \frac{1}{N_k}\sum_{j\in\text{cluster}_k}x_j$计算出每个cluster的新的中心点。
- 重复第二步,一直到迭代了最大的步数或者前后的$J$的值相差小于一个阈值为止。
NOTE:K-Means并不能保证全局最优,而且该算法得到的结果的好坏直接依赖于初始值的选取,当初始值选取不当时,最后得到的结果可能并不好,所以一般采用的方法是多次随机选取初始值,并选择结果最好的一次就行。
K-Means方法有一个很明显的局限就是它的距离衡量标准是高斯函数,所以只适用于特征是实数值的情形,而不能适用于当数据包含类型数据的情形。因此人们引入了K-Medoids算法。
K-Medoids算法在K-Means算法的基础上做出了如下两个改变:
- 将原来的目标函数$J$中的欧氏距离改为一个任意的dissimilarity measure函数$\mathcal{V}$:
\begin{equation} \tilde{J} = \sum_{n=1}^N\sum_{k=1}^K r_{nk}\mathcal{V}(x_n,\mu_k) \end{equation}
最常见的方式是构造一个dissimilarity matrix $\mathbf{D}$来代表$\mathcal{V}$,其中的元素$\mathbf{D}_{ij}$表示Object $i$和Object $j$之间的差异程度。
- 中心点的选取不再取同一Cluster数据的均值,而是从在已有的数据点里面选取的,具体而言,选一个到该Cluster中其他点距离之和最小的点。这使得K-Medoids算法不容易受到那些由于误差之类的原因产生的Outlier的影响,更加robust一些。
Spectral Clustering
Spectral Clustering(谱聚类)是一种基于图论的聚类方法,它能够识别任意形状的样本空间且收敛于全局最优解,其基本思想是利用样本数据的相似矩阵进行特征分解后得到的特征向量进行聚类,可见,它与样本feature无关而只与样本个数有关。
图的划分
图划分的目的是将有权无向图划分为两个或以上子图,使得子图规模差不多而割边权重之和最小。图的划分可以看做是有约束的最优化问题,它的目的是看怎么把每个点划分到某个子图中,比较不幸的是当你选择各种目标函数后发现该优化问题往往是NP-hard的。
怎么解决这个问题呢?松弛方法往往是一种利器(比如SVM中的松弛变量),对于图的划分可以认为能够将某个点的一部分划分在子图1中,另一部分划分在子图2中,而不是非此即彼,使用松弛方法的目的是将组合优化问题转化为数值优化问题,从而可以在多项式时间内解决之,最后在还原划分时可以通过阈值来还原,或者使用类似K-Means这样的方法,之后会有相关说明。
相关定义
- 用$G=(V,E)$表示无向图,其中$V$和$E$分别为其顶点集和边集;
- 说某条边属于某个子图是指该边的两个顶点都包含在子图中;
- 假设边$e$的两个不同端点为$i$和$j$,则该边的权重用$\omega_{i,j}$表示,对于无向无环图有$\omega_{i,j} = \omega_{j,i}$且$\omega_{i,i}=0$,为方便以下的“图”都指无向无环图;
- 对于图的某种划分方案$Cut$的定义为:所有两端点不在同一子图中的边的权重之和,它可以被看成该划分方案的损失函数,希望这种损失越小越好,本文以二分无向图为例,假设原无向图$G$被划分为$G_1$和$G_2$,那么有:
\begin{equation} Cut(G_1,G_2) = \sum_{i \in G_1,j \in G_2} \omega_{i,j} \end{equation}
Laplacian矩阵
假设无向图$G$被划分为$G_1$和$G_2$两个子图,该图的顶点数为:n=|V|,用$q$表示维指示向量,表明该划分方案,每个分量定义如下:
\begin{equation} q_i = \left \lbrace \begin{array}{cc} c_1 & i \in G_1 \\ c_2 & i \in G_2 \end{array} \right. \end{equation}
于是有:
\begin{equation} Cut(G_1,G_2) = \sum_{i \in G_1,j \in G_2} \omega_{i,j} = \frac{\sum_{i=1}^n \sum_{j=1}^n \omega_{i,j}(q_i-q_j)^2}{2(c_1-c_2)^2} \end{equation}
又因为:
\begin{equation} \begin{split} \sum_{i=1}^n \sum_{j=1}^n \omega_{i,j}(q_i-q_j)^2 &= \sum_{i=1}^n \sum_{j=1}^n \omega_{i,j}(q_i^2-2q_iq_j+q_j^2) \\ &= \sum_{i=1}^n \sum_{j=1}^n -2\omega_{i,j}q_iq_j + \sum_{i=1}^n \sum_{j=1}^n \omega_{i,j}(q_i^2+q_j^2) \\ &= \sum_{i=1}^n \sum_{j=1}^n -2\omega_{i,j}q_iq_j + \sum_{i=1}^n 2q_i^2(\sum_{j=1}^n \omega_{i,j}) \\ &=2q^T(D-W)q \end{split} \end{equation}
其中,$D$为对角矩阵,对角线元素为:
\begin{equation} D_{i,i} = \sum_{j=1}^n \omega_{i,j} \end{equation}
$W$为权重矩阵:$W_{i,j} = \omega_{i,j}$且$W_{i,i}=0$。
重新定义一个对称矩阵$L$,它便是Laplacian矩阵:
\begin{equation} L=D-W \end{equation}
矩阵元素为:
\begin{equation} L_{i,j} = \left \lbrace \begin{array}{cc} \sum_{j=1}^n \omega_{i,j} & i = j \\ -\omega_{i,j} & i \neq j \end{array} \right. \end{equation}
进一步观察:
\begin{equation} q^TLq = {1 \over 2} \sum_{i=1}^n \sum_{j=1}^n \omega_{i,j}(q_i-q_j)^2 \end{equation}
如果所有权重值都为非负,那么就有,这说明Laplacian矩阵是半正定矩阵;而当无向图为连通图时有特征值0且对应特征向量为$[1,1,1...1]^T$,这反映了,如果将无向图划分成两个子图,一个为其本身,另一个为空时,为0(当然,这种划分是没有意义的)。
其实上面推导的目的在于得到下面的关系:
\begin{equation} Cut(G_1,G_2) = \frac{q^TLq}{(c_1-c_2)^2} \end{equation}
这个等式的核心价值在于:将最小化划分的问题转变为最小化二次函数;从另一个角度看,实际上是把原来求离散值松弛为求连续实数值。
观察下图:
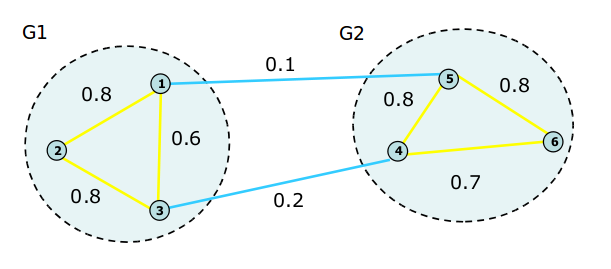
根据上图我们可以得到:
\begin{equation} W = \left[ \begin{array}{cc} 0.0 & 0.8 & 0.6 & 0.0 & 0.1 & 0.0 \\ 0.8 & 0.0 & 0.8 & 0.0 & 0.0 & 0.0 \\ 0.6 & 0.8 & 0.0 & 0.2 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.2 & 0.0 & 0.8 & 0.7 \\ 0.1 & 0.0 & 0.0 & 0.8 & 0.0 & 0.8 \\ 0.0 & 0.0 & 0.0 & 0.7 & 0.8 & 0.0 \end{array} \right] \end{equation}
\begin{equation} D = \left[ \begin{array}{cc} 1.5 & 0.0 & 0.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 1.6 & 0.0 & 0.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 1.6 & 0.0 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 1.7 & 0.0 & 0.0 \\ 0.0 & 0.0 & 0.0 & 0.0 & 1.7 & 0.0 \\ 0.0 & 0.0 & 0.0 & 0.0 & 0.0 & 1.5 \end{array} \right] \end{equation}
Laplacian矩阵为: \begin{equation} L = \left[ \begin{array}{cc} 1.5 & -0.8 & -0.6 & 0.0 & -0.1 & 0.0 \\ -0.8 & 1.6 & -0.8 & 0.0 & 0.0 & 0.0 \\ -0.6 & -0.8 & 1.6 & -0.2 & 0.0 & 0.0 \\ 0.0 & 0.0 & -0.2 & 1.7 & -0.8 & -0.7 \\ -0.1 & 0.0 & 0.0 & -0.8 & 1.7 & -0.8 \\ 0.0 & 0.0 & 0.0 & -0.7 & -0.8 & 1.5 \end{array} \right] \end{equation}
Laplacian矩阵是一种有效表示图的方式,任何一个Laplacian矩阵都对应一个权重非负地无向有权图,而满足以下条件的就是Laplacian矩阵:
- 为对称半正定矩阵,保证所有特征值都大于等于0;
- 矩阵有唯一的0特征值,其对应的特征向量为$[1,1,1...1]^T$,它反映了图的一种划分方式:一个子图包含原图所有端点,另一个子图为空。
划分方法
Minimum Cut方法
考虑最简单情况,另$C_1=1=-C_2$,无向图划分指示向量定义为:
\begin{equation} q_i = \left \lbrace \begin{array}{cc} 1 & i \in G_1 \\ -1 & i \in G_2 \end{array} \right. \end{equation}
要优化的目标为$Cut(G_1,G_2)$,由之前的推导可以将该问题松弛为以下问题:
\begin{equation} min \ q^TLq \\ s.t. [1,1,...1]^Tq=0 \\ q^Tq = n \end{equation}
从这个问题的形式可以联想到Rayleigh quotient:
\begin{equation} R(L,q) = \frac{q^TLq}{q^Tq} \end{equation}
原问题的最优解就是该Rayleigh quotient的最优解,而由Rayleigh quotient的性质可知:它的最小值,第二小值,......,最大值分别对应矩阵$L$的最小特征值,第二小特征值,......,最大特征值,且极值$q$在相应的特征向量处取得,即需要求解下特征系统的特征值和特征向量:
\begin{equation} Lq = \lambda q \end{equation}
这里需要注意约束条件$[1,1,...1]^Tq=0$,显然的最小特征值为0,此时对应特征向量为[1,1,...1]^T,不满足这个约束条件(剔除了无意义划分),于是最优解应该在第二小特征值对应的特征向量处取得。
当然,求得特征向量后还要考虑如何恢复划分,比如可以这样:特征向量分量值为正所对应的端点划分为$G_1$,反之划分为$G_2$;也可以这样:将特征向量分量值从小到大排列,以中位数为界划分$G_1$和$G_2$;还可以用K-Means算法聚类。
Ratio Cut方法
实际当中,划分图时除了要考虑最小化$Cut$外还要考虑划分的平衡性,为缓解出现类似一个子图包含非常多端点而另一个只包含很少端点的情况,出现了Ratio Cut,它衡量子图大小的标准是子图包含的端点个数。
定义$n_1$为子图1包含端点数,$n_2$为子图2包含端点数,$n_2=n-n_1$,则优化目标函数为:
\begin{equation} obj = Cut(G_1,G_2)(\frac{1}{n_1}+\frac{1}{n_2}) \end{equation}
其中:
\begin{equation} Cut(G_1,G_2) = \sum_{i \in G_1,j \in G_2} \omega_{i,j} \end{equation}
做一个简单变换:
\begin{equation} \begin{split} obj &= Cut(G_1,G_2)(\frac{1}{n_1}+\frac{1}{n_2}) = \sum_{i \in G_1,j \in G_2} \omega_{i,j}(\frac{1}{n_1}+\frac{1}{n_2}) \\ &= \sum_{i \in G_1,j \in G_2} \omega_{i,j}(\frac{n_1+n_2}{n_1n_2})=\sum_{i \in G_1,j \in G_2} \omega_{i,j}(\frac{(n_1+n_2)^2}{n_1n_2n}) \\ &= \sum_{i \in G_1,j \in G_2} \omega_{i,j}(\sqrt{\frac{n_1}{n_2n}}+\sqrt{\frac{n_2}{n_1n}})^2 \\ &= \sum_{i \in G_1,j \in G_2} \omega_{i,j}(q_i-q_j)^2 \end{split} \end{equation}
其中:
\begin{equation} q_i = \left \lbrace \begin{array}{cc} \sqrt{\frac{n_1}{n_2n}} & i \in G_1 \\ \sqrt{\frac{n_2}{n_1n}} & i \in G_2 \end{array} \right. \end{equation}
看吧,这形式多给力,原问题就松弛为下面这个问题了:
\begin{equation} min \ q^TLq \\ s.t. q^Te=0 \\ q^Tq = 1 \end{equation}
依然用Rayleigh quotient求解其第二小特征值及其特征向量。
NOTE:关于原问题为什么能松弛为上述形式,没看懂,望高人指点(Normalized Cut这部分也没完全懂)
Normalized Cut方法
与Ratio Cut类似,不同之处是,它衡量子图大小的标准是:子图各个端点的Degree之和。 定义:$d_1$为子图1Degree之和:
\begin{equation} d_1 = \sum_{i \in G_1} d_i \end{equation}
$d_2$为子图2Degree之和:
\begin{equation} d_2 = \sum_{i \in G_2} d_i \end{equation}
则优化目标函数为:
\begin{equation} \begin{split} obj = Cut(G_1,G_2)(\frac{1}{d_1}+\frac{1}{d_2}) = \sum_{i \in G_1,j \in G_2} \omega_{i,j}(q_i-q_j)^2 \end{split} \end{equation}
其中:
\begin{equation} q_i = \left \lbrace \begin{array}{cc} \sqrt{\frac{d_1}{d_2d}} & i \in G_1 \\ \sqrt{\frac{d_2}{d_1d}} & i \in G_2 \end{array} \right. \end{equation}
原问题就松弛为下面这个问题了:
\begin{equation} min \ q^TLq \\ s.t. q^De=0 \\ q^Dq = 1 \end{equation}
用泛化的Rayleigh quotient表示为:
\begin{equation} R(L,q) = \frac{q^TLq}{q^TDq} \end{equation}
那问题就变成求解下特征系统的特征值和特征向量:
\begin{equation} \begin{split} Lq &= \lambda Dq \\ &\Leftrightarrow Lq = \lambda D^{1 \over 2}D^{1 \over 2}q \\ &\Leftrightarrow D^{-\frac{1}{2}}LD^{-\frac{1}{2}}D^{1 \over 2}q = \lambda D^{1 \over 2}q \\ &\Leftrightarrow L\prime q\prime = \lambda q\prime \end{split} \end{equation}
其中,$L\prime = D^{-\frac{1}{2}}LD^{-\frac{1}{2}}$,$q\prime=D^{1 \over 2}q$ 显然,上式中最上面式子和最下面式子有相同的特征值,但是对应特征值的特征向量关系为:$q\prime=D^{1 \over 2}q$,因此我们可以先求最下面式子的特征值及其特征向量,然后为每个特征向量乘以$D^{-\frac{1}{2}}$就得到最上面式子的特征向量。
哦,对了,矩阵$L\prime = D^{-\frac{1}{2}}LD^{-\frac{1}{2}}$叫做Normalized Laplacian,因为它对角线元素值都为1。
Spectral Clustering
上边说了这么多,其实就是想将图的划分应用于聚类,而且这种聚类只需要样本的相似矩阵即可,把每个样本看成图中的一个顶点,样本之间的相似度看成由这两点组成的边的权重值,那么相似矩阵就是一幅有权无向图。对照图的划分方法,有下列两类Spectral Clustering算法,他们的区别在于Laplacian矩阵是否是规范化的:
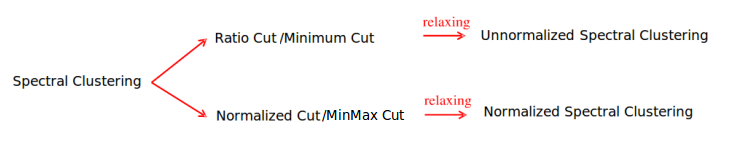
- Unnormalized Spectral Clustering算法
算法输入:样本相似矩阵$S$和要聚类的类别数$K$。
- 根据矩阵$S$建立权重矩阵$W$、三角矩阵$D$;
- 建立Laplacian矩阵$L$;
- 求矩阵$L$的前$K$小个特征值及其对应的特征向量,注意最小的那个特征值一定是0且对应的特征向量为[1,1,...1]^T;
- 以这K组特征向量组成新的矩阵,其行数为样本数,列数为$K$,这里就是做了降维操作,从$N$维降到$K$维,(实际上除去那个全为1的向量维度降为了$K-1$);
-
使用K-Means算法进行聚类,得到$K$个Cluster。
-
Normalized Spectral Clustering算法
算法输入:样本相似矩阵$S$和要聚类的类别数$K$。
- 根据矩阵$S$建立权重矩阵$W$、三角矩阵$D$;
- 建立Laplacian矩阵$L$以及$L\prime = D^{-\frac{1}{2}}LD^{-\frac{1}{2}}$;
- 求矩阵$L\prime$的前$K$小个特征值及其对应的特征向量,注意最小的那个特征值一定是0且对应的特征向量为$[1,1...1]^T$;
- 利用$q\prime=D^{1 \over 2}q$求得矩阵$L$前$K$小个特征向量;
- 以这$K$组特征向量组成新的矩阵,其行数为样本数$N$,列数为$K$;
- 使用K-Means算法进行聚类,得到$K$个Cluster。
源码实现
以下我们给出Unnormalized Spectral Clustering的Python源码实现:
import sys
import numpy as np
import matplotlib.pyplot as plt
from scipy.linalg import eig
from scipy.cluster.vq import kmeans2
from scipy.sparse.linalg import eigen
from scipy.spatial.kdtree import KDTree
def get_noise(stddev=0.25, numpoints=150):
# 2d gaussian random noise
x = np.random.normal(0, stddev, numpoints)
y = np.random.normal(0, stddev, numpoints)
return np.column_stack((x, y))
def get_circle(center=(0.0, 0.0), r=1.0, numpoints=150):
# use polar coordinates to get uniformly distributed points
step = np.pi * 2.0 / numpoints
t = np.arange(0, np.pi * 2.0, step)
x = center[0] + r * np.cos(t)
y = center[1] + r * np.sin(t)
return np.column_stack((x, y))
def radial_kernel(c=1.5):
def inner(a, b):
d = a - b
return np.exp((-1 * (np.sqrt(np.dot(d, d.conj()))**2)) / c)
return inner
def circle_samples():
"Generate noisy circle points"
circles = []
for radius in (1.0, 2.8, 5.0):
circles.append(get_circle(r=radius) + get_noise())
return np.vstack(circles)
def mutual_knn(points, n=10, distance=radial_kernel()):
knn = {}
kt = KDTree(points)
for i, point in enumerate(points):
# cannot use euclidean distance directly
for neighbour in kt.query(point, n + 1)[1]:
if i != neighbour:
knn.setdefault(i, []).append(
(distance(point, points[neighbour]), neighbour))
return knn
def get_distance_matrix(knn):
n = len(knn)
W = np.zeros((n, n))
for point, nearest_neighbours in knn.iteritems():
for distance, neighbour in nearest_neighbours:
W[point][neighbour] = distance
return W
def rename_clusters(idx):
# so that first cluster has index 0
num = -1
seen = {}
newidx = []
for id in idx:
if id not in seen:
num += 1
seen[id] = num
newidx.append(seen[id])
return np.array(newidx)
def cluster_points(L):
# sparse eigen is a little bit faster than eig
#evals, evcts = eigen(L, k=15, which="SM")
evals, evcts = eig(L)
evals, evcts = evals.real, evcts.real
edict = dict(zip(evals, evcts.transpose()))
evals = sorted(edict.keys())
# second and third smallest eigenvalue + vector
Y = np.array([edict[k] for k in evals[1:3]]).transpose()
res, idx = kmeans2(Y, 3, minit='random')
return evals[:15], Y, rename_clusters(idx)
def change_tick_fontsize(ax, size):
for tl in ax.get_xticklabels():
tl.set_fontsize(size)
for tl in ax.get_yticklabels():
tl.set_fontsize(size)
def get_colormap():
# map cluster label to color (0, 1, 2) -> (orange, blue, green)
from matplotlib.colors import ListedColormap
orange = (0.918, 0.545, 0.0)
blue = (0.169, 0.651, 0.914)
green = (0.0, 0.58, 0.365)
return ListedColormap([orange, blue, green])
def plot_circles(ax, points, idx, colormap):
plt.scatter(points[:,0], points[:,1], s=10, c=idx, cmap=colormap,
alpha=0.9, facecolors="none")
plt.xlabel("x1", fontsize=8)
plt.ylabel("x2", fontsize=8)
change_tick_fontsize(ax, 8 )
plt.ylim(-6, 6)
plt.xlim(-6, 6)
def plot_eigenvalues(ax, evals):
plt.scatter(np.arange(0, len(evals)), evals,
c=(0.0, 0.58, 0.365), linewidth=0)
plt.xlabel("Number", fontsize=8)
plt.ylabel("Eigenvalue", fontsize=8)
plt.axhline(0, ls="--", c="k")
change_tick_fontsize(ax, 8 )
def plot_eigenvectors(ax, Y, idx, colormap):
from matplotlib.ticker import MaxNLocator
from mpl_toolkits.axes_grid import make_axes_locatable
divider = make_axes_locatable(ax)
ax2 = divider.new_vertical(size="100%", pad=0.05)
fig1 = ax.get_figure()
fig1.add_axes(ax2)
ax2.set_title("Eigenvectors", fontsize=10)
ax2.scatter(np.arange(0, len(Y)), Y[:,0], s=10, c=idx, cmap=colormap,
alpha=0.9, facecolors="none")
ax2.axhline(0, ls="--", c="k")
ax2.yaxis.set_major_locator(MaxNLocator(4))
ax.yaxis.set_major_locator(MaxNLocator(4))
ax.axhline(0, ls="--", c="k")
ax.scatter(np.arange(0, len(Y)), Y[:,1], s=10, c=idx, cmap=colormap,
alpha=0.9, facecolors="none")
ax.set_xlabel("index", fontsize=8)
ax2.set_ylabel("2nd Smallest", fontsize=8)
ax.set_ylabel("3nd Smallest", fontsize=8)
change_tick_fontsize(ax, 8 )
change_tick_fontsize(ax2, 8 )
for tl in ax2.get_xticklabels():
tl.set_visible(False)
def plot_spec_clustering(ax, Y, idx, colormap):
plt.title("Spectral Clustering", fontsize=10)
plt.scatter(Y[:,0], Y[:,1], c=idx, cmap=colormap, s=10, alpha=0.9,
facecolors="none")
plt.xlabel("Second Smallest Eigenvector", fontsize=8)
plt.ylabel("Third Smallest Eigenvector", fontsize=8)
change_tick_fontsize(ax, 8 )
def plot_figure(points, evals, Y, idx):
colormap = get_colormap()
fig = plt.figure(figsize=(6, 5.5))
fig.subplots_adjust(wspace=0.4, hspace=0.3)
ax = fig.add_subplot(2, 2, 1)
plot_circles(ax, points, idx, colormap)
ax = fig.add_subplot(2, 2, 2)
plot_eigenvalues(ax, evals)
ax = fig.add_subplot(2, 2, 3)
plot_eigenvectors(ax, Y, idx, colormap)
ax = fig.add_subplot(2, 2, 4)
plot_spec_clustering(ax, Y, idx, colormap)
plt.show()
def main(args):
points = circle_samples()
knn_points = mutual_knn(points)
W = get_distance_matrix(knn_points)
G = np.diag([sum(Wi) for Wi in W])
# unnormalized graph Laplacian
L = G - W
evals, Y, idx = cluster_points(L)
plot_figure(points, evals, Y, idx)
if __name__ == "__main__":
main(sys.argv)
运行源码得到下图:
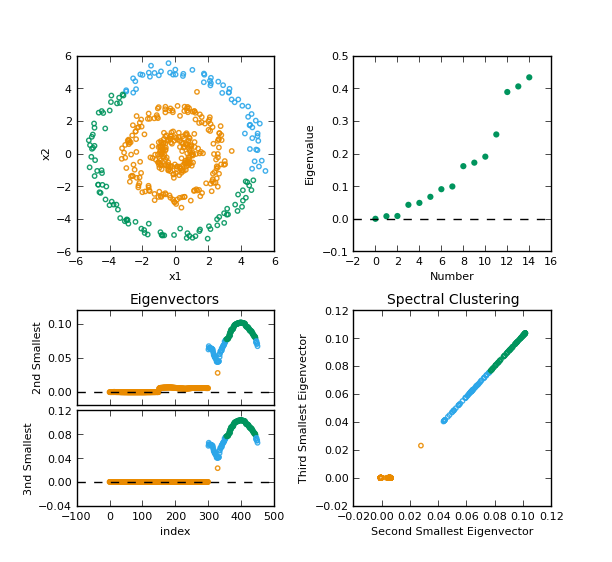
总结
- 图划分问题中的关键点在于选择合适的指示向量并将其进行松弛化处理,从而将最小化划分的问题转变为最小化二次函数,进而转化为求Rayleigh quotient极值的问题;
-
Spectral Clustering的各个阶段为:
- 选择合适的相似性函数计算相似度矩阵;
- 计算矩阵L的特征值及其特征向量,比如可以用
Lanczos迭代算法; - 如何选择K,可以采用启发式方法,比如,发现第1到m的特征值都挺小的,到了m+1突然变成较大的数,那么就可以选择K=m;
- 用K-Means算法聚类,当然它不是唯一选择;
- Normalized Spectral Clustering在让Cluster间相似度最小而Cluster内部相似度最大方面表现要更好,所以首选这类方法。
Hierarchical Clustering
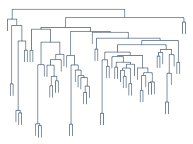
Hierarchical Clustering正如它字面上的意思那样,是层次化的聚类,得出来的结构是一棵树,如上图所示。在前面我们介绍过不少聚类方法,但是都是“平坦”型的聚类,然而他们还有一个更大的共同点,或者说是弱点,就是难以确定类别数。我们这里要说的Hierarchical Clustering则从某种意义上来说也算是解决了这个问题,因为在做Clustering的时候并不需要知道类别数,而得到的结果是一棵树,事后可以在任意的地方横切一刀,得到指定数目的cluster,按需取即可。
听上去很诱人,不过其实Hierarchical Clustering的想法很简单,主要分为两大类:Agglomerative(自底向上)和Divisive(自顶向下)。首先说前者,自底向上,一开始,每个数据点各自为一个类别,然后每一次迭代选取距离最近的两个类别,把他们合并,直到最后只剩下一个类别为止,至此一棵树构造完成。
看起来很简单吧?其实确实也是比较简单的,不过还是有两个问题需要先说清除才行:
- 如何计算两个点的距离?这个通常是problem dependent的,一般情况下可以直接用一些比较通用的距离就可以了,比如欧氏距离等。
-
如何计算两个类别之间的距离?一开始所有的类别都是一个点,计算距离只是计算两个点之间的距离,但是经过后续合并之后,一个类别里就不止一个点了,那距离又要怎样算呢?到这里又有三个变种:
- Single Linkage:又叫做nearest-neighbor,就是取两个集合中距离最近的两个点的距离作为这两个集合的距离,容易造成一种叫做Chaining的效果,两个cluster明明从“大局”上离得比较远,但是由于其中个别的点距离比较近就被合并了,并且这样合并之后Chaining效应会进一步扩大,最后会得到比较松散的cluster 。
- Complete Linkage:这个则完全是Single Linkage的反面极端,取两个集合中距离最远的两个点的距离作为两个集合的距离。其效果也是刚好相反的,限制非常大,两个cluster即使已经很接近了,但是只要有不配合的点存在,就顽固到底,老死不相合并,也是不太好的办法。
- Group Average:这种方法看起来相对有道理一些,也就是把两个集合中的点两两的距离全部放在一起求一个平均值,相对也能得到合适一点的结果。
总的来说,一般都不太用Single Linkage或者Complete Linkage这两种过于极端的方法。整个agglomerative hierarchical clustering 的算法就是这个样子,描述起来还是相当简单的,不过计算起来复杂度还是比较高的,要找出距离最近的两个点,需要一个双重循环,而且 Group Average计算距离的时候也是一个双重循环。
另外,需要提一下的是本文一开始的那个树状结构图,它有一个专门的称呼,叫做Dendrogram,其实就是一种二叉树,画的时候让子树的高度和它两个后代合并时相互之间的距离大小成比例,就可以得到一个相对直观的结构概览。
Agglomerative clustering差不多就这样了,再来看Divisive clustering,也就是自顶向下的层次聚类,这种方法并没有Agglomerative clustering这样受关注,大概因为把一个节点分割为两个并不如把两个节点结合为一个那么简单吧,通常在需要做hierarchical clustering 但总体的cluster数目又不太多的时候可以考虑这种方法,这时可以分割到符合条件为止,而不必一直分割到每个数据点一个cluster 。
总的来说,Divisive clustering 的每一次分割需要关注两个方面:一是选哪一个cluster来分割;二是如何分割。关于cluster的选取,通常采用一些衡量松散程度的度量值来比较,例如cluster中距离最远的两个数据点之间的距离,或者cluster中所有节点相互距离的平均值等,直接选取最“松散”的一个cluster来进行分割。而分割的方法也有多种,比如,直接采用普通的flat clustering算法(例如K-Means来进行二类聚类,不过这样的方法计算量变得很大,而且像K-Means 这样的和初值选取关系很大的算法,会导致结果不稳定。另一种比较常用的分割方法(简而言之就是一个排除异己的过程)如下:
- 待分割的cluster记为$G$,在$G$中取出一个到其他点的平均距离最远的点$x$,构成新cluster H;
- 在 G 中选取这样的点$x\prime$,$x\prime$到$G$中其他点的平均距离减去$x\prime$到$H$中所有点的平均距离这个差值最大,将其归入$H$中;
- 重复上一个步骤,直到差值为负。
到此为止,关于Hierarchical clustering介绍就结束了。总的来说,Hierarchical clustering算法似乎都是描述起来很简单,计算起来很困难(计算量很大)。并且,不管是Agglomerative还是 Divisive 实际上都是贪心算法了,也并不能保证能得到全局最优的。而得到的结果,虽然说可以从直观上来得到一个比较形象的大局观,但是似乎实际用处并不如众多Flat clustering 算法那么广泛。
参考文献
- Rand Index
- 漫谈 Clustering (1): k-means
- 漫谈 Clustering (2): k-medoids
- Spectral Clustering
- Machine Learning:A Probabilistic Perspective(Chapter 25)