貌似感冒了,脑子昏昏沉沉的,啥都想不了,无意中发现这么一个高端大气上档次的算法---局部敏感哈希方法。于是Google了一下,发现这篇Locality Sensitive Hashing(LSH)之随机投影法关于局部敏感哈希算法的介绍还不错,于是摘录如下:

概述

LSH是由文献[1]提出的一种用于高效求解最近邻搜索问题的Hash算法。LSH算法的基本思想是利用一个hash函数把集合中的元素映射成hash值，使得相似度越高的元素hash值相等的概率也越高。LSH算法使用的关键是针对某一种相似度计算方法，找到一个具有以上描述特性的hash函数。LSH所要求的hash函数的准确数学定义比较复杂，以下给出一种通俗的定义方式：

对于集合$S$，集合内元素间相似度的计算公式为$sim(a,b)$。如果存在一个hash函数$h()$满足以下条件：存在一个相似度$s$到概率$p$的单调递增映射关系，使得$S$中的任意两个满足$sim(a,b)\geq s$的元素$a$和$b$，$h(a)=h(b)$的概率大于等于$p$。那么$h()$就是该集合的一个LSH算法hash函数。

一般来说在最近邻搜索中，元素间的关系可以用相似度或者距离来衡量。如果用距离来衡量，那么距离一般与相似度之间存在单调递减的关系。以上描述如果使用距离来替代相似度需要在单调关系上做适当修改。

根据元素相似度计算方式的不同，LSH有许多不同的hash算法。两种比较常见的hash算法是随机投影法和min-hash算法。本文即将介绍的随机投影法适用于集合元素可以表示成向量的形式，并且相似度计算是基于向量之间夹角的应用场景，如余弦相似度。min-hash法在参考文献[2]中有相关介绍。

随机投影法(Random projection)

假设集合$S$中的每个元素都是一个$n$维的向量：

\begin{equation} \vec{x} ={v_1,v_2,\cdots,v_n} \end{equation}

集合中两个元素$\vec{v}$和$\vec{u}$之间的相似度定义为:

\begin{equation} sim(\vec{v},\vec{u})=\frac{\vec{v}*\vec{u}}{|\vec{v}||\vec{u}|} \end{equation}

对于以上元素集合$S$的随机投影法hash函数$h()$可以定义为如下：

在$n$维空间中随机选取一个非零向量$\vec{x}={x_1, x_2, \ldots, x_n}$。考虑以该向量为法向量且经过坐标系原点的超平面，该超平面把整个$n$维空间分成了两部分，将法向量所在的空间称为正空间，另一空间为负空间。那么集合$S$中位于正空间的向量元素hash值为1，位于负空间的向量元素hash值为0。判断向量属于哪部分空间的一种简单办法是判断向量与法向量之间的夹角为锐角还是钝角，因此具体的定义公式可以写为

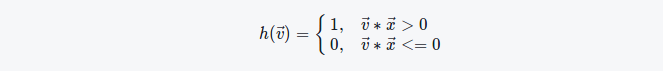
Formula 1

根据以上定义，假设向量$\vec{v}$和$\vec{u}$之间的夹角为$\theta$，由于法向量$\vec{x}$是随机选取的，那么这两个向量未被该超平面分割到两侧（即hash值相等）的概率应该为：$p(\theta)=1-\frac{\theta}{\pi}$。假设两个向量的相似度值为$s$，那么根据$\theta=arccos(s)$,有

\begin{equation} p(s)=1-\frac{arccos(s)}{\pi} \end{equation}

因此，存在相似度$s$到概率$p$的单调递增映射关系，使得对于任意相似度大于等于$s$的两个元素，它们hash值相等的概率大于等于$p(s)$。所以，以上定义的hash值计算方法符合LSH算法的要求。

以上所描述的$h()$函数虽然符合LSH算法的要求，但是实用性不高。因为该hash函数只产生了两个hash值，没有达到hash函数将元素分散到多个分组的目的。为了增加不同hash值的个数，可以多次生成独立的函数$h()$，只有当两个元素的多个$h()$值都相等时才算拥有相同的hash值。根据该思路可以定义如下的hash函数$H()$：

\begin{equation} H(\vec{v})=(h_b(\vec{v})h_{b-1}(\vec{v})\ldots h_1(\vec{v}))_2 \end{equation}

其中每个$h_i(\vec{v})$表示一个独立的$h()$函数，$H()$函数值的二进制表现形式中每一位都是一个$h()$函数的结果。以$H()$为hash函数的话，两个相似度为$s$的元素具有相同hash值的概率公式为

\begin{equation} p(s)=(1-\frac{arccos(s)}{\pi})^b \end{equation}

hash值的个数为$2^b$。很容易看出$H()$函数同样也是符合LSH算法要求的。一般随机按投影算法选用的hash函数就是$H()$。其中参数$b$的取值会在后面小节中讨论。

随机投影法在最近邻搜索中的应用

随机投影法提高执行速度

这里我们介绍当集合$T$的元素和查询元素$q$为同维度向量(维度为$n$)，并且元素相似度计算方法为余弦相似度时，使用随机投影法来提高最近邻搜索的执行速度。具体的实现方法为：

预处理阶段:使用hash函数$H(*)$计算集合$T$中所有元素的hash值，将集合$T$分成一个个分组，每个分组内的元素hash值均相等。用合适的数据结构保存这些hash值到分组的映射关系（如HashMap）。
查询阶段:计算查询元素$q$的hash值$H(q)$，取集合$T$中所有hash值为$H(q)$的分组，以该分组内的所有元素作为候选集合，在候选该集合内使用简单的最近邻搜索方法寻找最相似的$k$个元素。

该方法的执行效率取决于$H(*)$的hash值个数$2^b$，也就是分组的个数。理想情况下，如果集合$T$中的向量元素在空间中分布的足够均匀，那么每一个hash值对应的元素集合大小大致为$\frac{m} {2^b}$。当$m$远大于向量元素的维度时，每次查询的速度可以提高到$2^b$倍。

根据以上分析$H()$中$b$的取值越大算法的执行速度的提升越多，并且是指数级别的提升。但是，在这种情况下$H()$函数下的概率公式$p(s)$，实际上表示与查询元素$q$的相似度为$s$的元素的召回率。当$b$的取值越大时，top k元素的召回率必然会下降。因此算法执行速度的提升需要召回率的下降作为代价。例如：当$b$等于10时，如果要保证某个元素的召回率不小于0.9，那么该元素与查询元素$q$的相似度必须不小于0.9999998。

提高召回率改进

为了在保证召回率的前提下尽可能提高算法的执行效率，一般可以进行如下改进：

预处理阶段:生成$t$个独立的hash函数$H_i(∗)$，根据这$t$个不同的hash函数，对集合$T$进行$t$种不同的分组，每一种分组方式下，同一个分组的元素在对应hash函数下具有相同的hash值。用合适的数据结构保存这些映射关系（如使用$t$个HashMap来保存）。
查询阶段:对于每一个hash函数$H_i(∗)$，计算查询元素$q$的hash值$H_i(q)$，将集合$T$中$H_i(∗)$所对应的分组方式下hash值为$H_i(q)$的分组添加到该次查询的候选集合中。然后，在该候选集合内使用简单的最近邻搜索方法寻找最相似的$k$个元素。

以上改进使得集合中元素与查询元素$q$的$t$个hash值中，只要任意一个相等，那么该集合元素就会被加入到候选集中。那么，相似度为$s$的元素的召回率为

\begin{equation} p(s)=1-(1-(1-\frac{arccos(s)}{\pi})^b)^t \end{equation}

在执行效率上，预处理阶段由于需要计算$t$个hash函数的值，所以执行时间上升为$t$倍。查询阶段，如果单纯考虑候选集合大小对执行效率的影响，在最坏的情况下，$t$个hash值获得的列表均不相同，候选集集合大小的期望值为$\frac{t∗m}{2^b}$，查询速度下降至$1 \over t$，与简单近邻搜索相比查询速度提升为$\frac{2^b}{t}$倍。

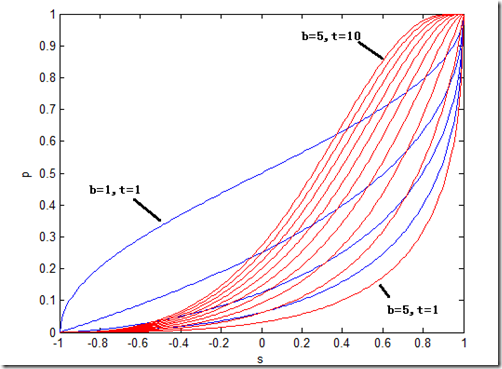
下图是召回率公式$p(s)=1-(1-(1-\frac{arccos(s)}{\pi})^b)^t$在不同的$b$和$t$取值下的$s-p$曲线。我们通过这些曲线来分析这里引入参数$t$的意义。4条蓝色的线以及最右边红色的线表示当$t$取值为1（相当于没有引入$t$），而$b$的取值从1变化到5的过程，从图中可以看出随着$b$的增大，不同相似度下的召回率都下降的非常厉害，特别的，当相似度接近1时曲线的斜率很大，也就说在高相似度的区域，召回率对相似度的变化非常敏感。10条红色的线从右到左表示$b$的取值为5不变，$t$的取值从1到10的过程，从图中可以看出，随着$t$的增大，曲线的形状发生了变化，高相似度区域的召回率变得下降的非常平缓，而最陡峭的地方渐渐的被移动到相对较低的相似度区域。因此，从以上曲线的变化特点可以看出，引入适当的参数$t$使得高相似度区域在一段较大的范围内仍然能够保持很高的召回率从而满足实际应用的需求。

SP Curve

参数选取

根据以上分析，$H(*)$函数的参数$b$越大查询效率越高，但是召回率越低；参数$t$越大查询效率越低但是召回率越高。因此选择适当参数$b$和$t$来折中查询效率与召回率之间的矛盾是应用好随机投影法的关键。下面提供一种在实际应用中选取$b$和$t$的参考方法。

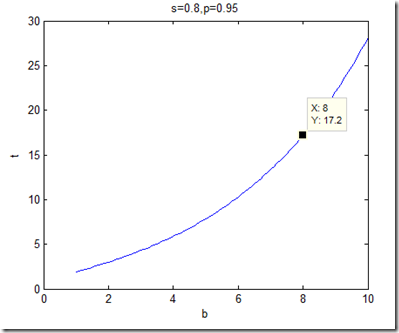
根据实际应用的需要确定一对$(s,p)$，表示相似度大于等于$s$的元素，召回率的最低要求为$p$。然后将召回率公式表示成$b-t$之间的函数关系$t=\log_{1-(1-\frac{acos(s)}{pi})^b}{(1-p)}$。根据$(s,p)$的取值，画出$b-t$的关系曲线。如$s=0.8,p=0.95$时的$b-t$曲线如下图所示。考虑具体应用中的实际情况，在该曲线上选取一组使得执行效率可以达到最优的$(b,t)$组合。

BT_Curve

关于最近邻文本搜索

在最近邻文本搜索中，一般待检索的文本或查询文本，都已被解析成一系列带有权重的关键词，然后通过余弦相似度公式计算两个文本之间的相似度。这种应用场景下的最近邻搜索与以上所提到的最近邻搜索问题相比存在以下两个特点：

如果把每个文本的带权重关键词表都看作是一个向量元素的话，每个关键词都是向量的一个维度，关键词权重为该维度的值。理论上可能关键词的个数并不确定（所有单词的组合都可能是一个关键词），因此该向量元素的维数实际上是不确定的。
由于关键词权重肯定是大于零的，所以向量元素的每一个维度的值都是非负的。

对于第一个特点，我们需要选取一个包含$n$个关键词的关键词集合，在进行文本相似度计算时只考虑属于该集合的关键词。也就是说，每一个文本都视为是一个$n$维度的向量，关键词权重体现为对应维度的值。该关键词集合可以有很多种生成办法，比如可以是网站上具有一定搜索频率的关键词集合，总的来说该关键词集合应当能够涵盖所有有意义并且具有一定使用频率的关键词。通常$n$的取值会比较大，如几十万到几百万，由于在使用随机投影算法时，每一个生成的随机向量维度都为$n$，这种情况下需要特别考虑利用这些高维随机向量对执行效率造成的影响，在确定$b、t$参数时需要考虑到这方面的影响。

对于第二个特点，由于向量元素各维度值都非负，那么这些元素在高维空间中只会出现在特定的区域中。比如当$n$为3时，只会出现在第一象限中。一个直观的感觉是在生成随机向量的时候，会不会生成大量的无用切割平面（与第一个象限空间不相交，使得所有元素都位于切割平面的同侧）。这些切割平面对应的$H(*)$函数hash值中的二进制位恒定为1或者0，对于提高算法执行速度没有帮助。以下说明这种担心是没有必要的：

切割平面与第一象限空间不相交等价于其法向量的每一个维度值都有相同的符号（都为正或者负），否则总能在第一象限空间中找到两个向量与法向量的乘积符号不同，也就是在切割平面的两侧。那么，随机生成的n维向量所有维度值都同号的概率为$\frac{1}{2^{n−1}}$，当$n$的取值很大时，该概率可以忽略不计。

参考文献

[1] P. Indyk and R. Motwani. Approximate Nearest Neighbor:Towards Removing the Curse of Dimensionality. In Proc. of the 30th Annual ACM Symposium on Theory of Computing, 1998, pp. 604–613.

[2] Google News Personalization: Scalable Online Collaborative Filtering.

Comment

当最近邻遇到LSH

概述