计算机视觉(II):边缘检测
本文中的介绍相对粗浅,自己实现一遍这些算法可能会有更为深入的了解,理论部分也不是很充分,没有那种"边缘检测不过如此"的感觉,以后可能就这个问题进行更为深入的挖掘(如果时间允许的话).此外,本文中对Canny边缘的非极大值抑制也没有给出解释,有机会我们会详细讨论。
边缘
边缘(edge)是指图像局部强度变化最显著的部分。主要存在于目标与目标、目标与背景、区域与区域(包括不同色彩)之间,是图像分割、纹理特征和形状特征等图像分析的重要基础。
图像强度的显著变化可分为:
- 阶跃变化函数,即图像强度在不连续处的两边的像素灰度值有着显著的差异;
- 线条(屋顶)变化函数,即图像强度突然从一个值变化到另一个值,保持一较小行程后又回到原来的值。
图像的边缘有方向和幅度两个属性,沿边缘方向像素变化平缓,垂直于边缘方向像素变化剧烈.边缘上的这种变化可以用微分算子检测出来,通常用一阶或二阶导数来检测边缘。
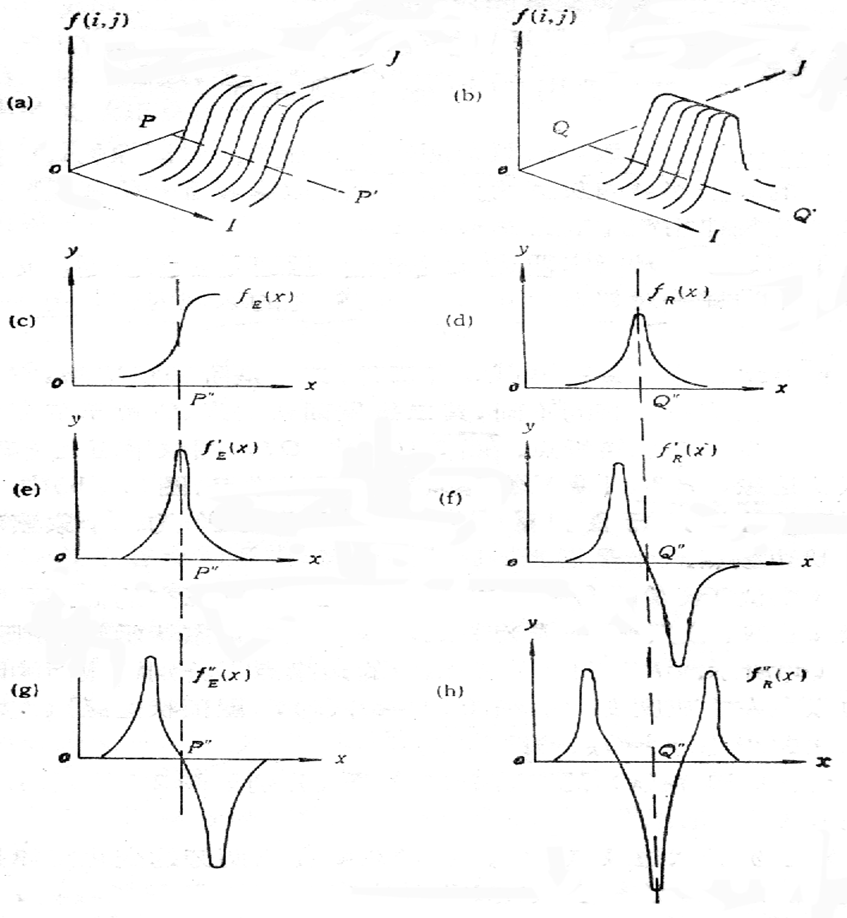
注:(a)(b)分别是阶跃函数和屋顶函数的二维图像;(c)(d)是阶跃和屋顶函数的函数图象;(e)(f)对应一阶导数;(g)(h)是二阶导数。
一阶导数法:梯度算子
对于左图,左侧的边是正的(由暗到亮),右侧的边是负的(由亮到暗)。对于右图,结论相反。常数部分为零。用来检测边是否存在。
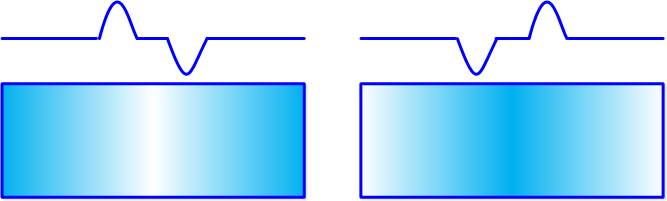
梯度算子 Gradient operators
函数$f(x,y)$在$(x,y)$处的梯度为一个向量:
\begin{equation} \bigtriangledown f = [\frac{\partial f}{\partial x},\frac{\partial f}{\partial y}]^T \end{equation}
计算这个向量的大小为:
\begin{equation} |\bigtriangledown f| = mag(\bigtriangledown f) = [(\frac{\partial f}{\partial x})^2+(\frac{\partial f}{\partial y})^2]^{1 \over 2} \end{equation}
近似为:
\begin{equation} |\bigtriangledown f| \thickapprox |G_x| + |G_y| \end{equation}
梯度的方向角为:
\begin{equation} a(x,y) = arctan(\frac{G_y}{G_x}) \end{equation}
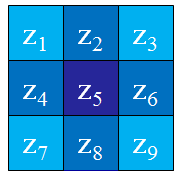
Sobel算子
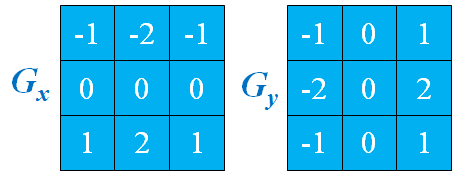
Sobel算子的表示:
\begin{equation} \begin{split} G_x &= (z_7+2z_8+z_9) - (z_1+2z_2+z_3) \\ G_y &= (z_3+2z_6+z_9) - (z_1+2z_4+z_7) \end{split} \end{equation}
梯度幅值:
\begin{equation} |\bigtriangledown f| \thickapprox |G_x| + |G_y| \end{equation}
用卷积模板来实现:
二阶微分法:拉普拉斯
二阶微分在亮的一边是负的,在暗的一边是正的。常数部分为零。可以用来确定边的准确位置,以及像素在亮的一侧还是暗的一侧。
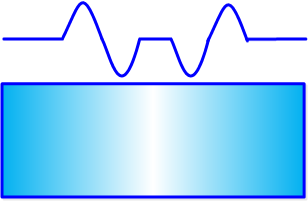
LapLace 拉普拉斯算子
二维函数$f(x,y)$的拉普拉斯是一个二阶的微分,定义为:
\begin{equation} \bigtriangledown^2 f = \frac{\partial^2 f}{\partial x^2}+\frac{\partial^2 f}{\partial y^2} \end{equation}
其中:
\begin{equation} \begin{split} \frac{\partial^2 f}{\partial x^2} &= f[x+1,y]-2f[x,y]+f[x-1,y] \\ \frac{\partial^2 f}{\partial y^2} &= f[x,y+1]-2f[x,y]+f[x,y-1] \end{split} \end{equation}
可以用多种方式将其表示为数字形式。对于一个3*3的区域,经验上被推荐最多的形式是:
\begin{equation} \bigtriangledown^2 f = 4z_5 - (z_2+z_4+z_6+z_8) \end{equation}
定义数字形式的拉普拉斯要求系数之和必为0
以下给出两种边缘检测算子的代码示例:
#include <iostream>
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
using namespace std;
using namespace cv;
int main()
{
Mat src, src_gray;
Mat grad;
int scale = 1;
int delta = 0;
int ddepth = CV_16S;
int kernel_size = 3;
/// Load an image
src = imread("/home/qingyuanxingsi/workspace/C++/contents/lufei.jpg");
if( !src.data )
{ return -1; }
GaussianBlur( src, src, Size(3,3), 0, 0, BORDER_DEFAULT );
cvtColor( src, src_gray, CV_RGB2GRAY );
/////////////////////////// Sobe l////////////////////////////////////
/// Generate grad_x and grad_y
Mat grad_x, grad_y;
Mat abs_grad_x, abs_grad_y;
/// Gradient X
//Scharr( src_gray, grad_x, ddepth, 1, 0, scale, delta, BORDER_DEFAULT );
//Calculates the first, second, third, or mixed image derivatives using an extended Sobel operator.
Sobel( src_gray, grad_x, ddepth, 1, 0, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_x, abs_grad_x );
/// Gradient Y
//Scharr( src_gray, grad_y, ddepth, 0, 1, scale, delta, BORDER_DEFAULT );
Sobel( src_gray, grad_y, ddepth, 0, 1, 3, scale, delta, BORDER_DEFAULT );
convertScaleAbs( grad_y, abs_grad_y );
/// Total Gradient (approximate)
addWeighted( abs_grad_x, 0.5, abs_grad_y, 0.5, 0, grad );
namedWindow("Sobel", CV_WINDOW_AUTOSIZE );
imshow("Sobel", grad );
imwrite("Sobel.png",grad);
/////////////////////////////////// Laplace ///////////////////////////////
Mat abs_dst,dst;
Laplacian( src_gray, dst, ddepth, kernel_size, scale, delta, BORDER_DEFAULT );
convertScaleAbs( dst, abs_dst );
namedWindow("Laplacian", CV_WINDOW_AUTOSIZE );
imshow("Laplacian", abs_dst );
imwrite("Laplace.png",grad);
waitKey(0);
return 0;
}
源图我们采用海贼王路飞图像:

Sobel算子处理后得到如下边缘:

Sobel算子可以直接计算$G_x$ 、$G_y$可以检测到边的存在,以及从暗到亮,从亮到暗的变化。仅计算$|G_x|$,产生最强的响应是正交于$x$轴的边;$|G_y|$则是正交于$y$轴的边。
Laplacian算子则得到如下边缘:

拉普拉斯对噪声敏感,会产生双边效果。不能检测出边的方向。通常不直接用于边的检测,只起辅助的角色,检测一个像素是在边的亮的一边还是暗的一边利用零跨越,确定边的位置。
Canny边缘检测
在计算机视觉边缘检测算法实现时,实际上就是将图像与某边缘检测模板做卷积的过程。针对Canny而言,其卷积模板相对来说比较简单:
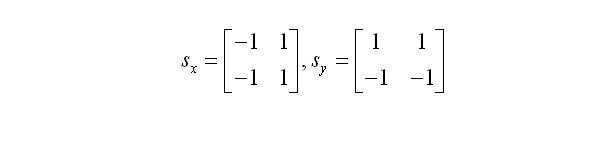
我们将左上角视为$f[i,j]$,则其$x$,$y$方向的偏导数矩阵,梯度幅值以及方向的表达式分别为:
\begin{equation} \begin{split} P[i,j] &= (f[i,j+1]+f[i+1,j+1)-f[i][j]-f[i+1,j])/2 \\ Q[i,j] &= (f[i,j]+f[i][j+1]-f[i+1,j]-f[i+1,j+1])/2 \\ M[i,j] &= \sqrt{P]i,j]^2+Q[i,j]^2} \\ \theta[i,j] &= arctan(\frac{Q[i,j]}{P[i,j]}) \end{split} \end{equation}
对梯度幅值进行非极大值抑制[TODO]
用双阈值算法检测和连接边缘
Canny算法中减少假边缘数量的方法是采用双阈值法。选择两个阈值,根据高阈值得到一个边缘图像,这样一个图像含有很少的假边缘,但是由于阈值较高,产生的图像边缘可能不闭合,为解决这样一个问题采用了另外一个低阈值。
在高阈值图像中把边缘链接成轮廓,当到达轮廓的端点时,该算法会在断点的8邻域点中寻找满足低阈值的点,再根据此点收集新的边缘,直到整个图像边缘闭合。
以上即为Canny边缘检测算法的原理分析,接下来我们给出一个OpenCV代码示例。
#include <iostream>
#include "opencv2/core/core.hpp"
#include "opencv2/imgproc/imgproc.hpp"
#include "opencv2/highgui/highgui.hpp"
using namespace std;
using namespace cv;
Mat src, src_gray;
Mat dst, detected_edges;
int edgeThresh = 1;
int lowThreshold;
int const max_lowThreshold = 100;
int ratio = 3;
int kernel_size = 3;
char* window_name = "Canny";
void CannyThreshold(int, void*)
{
/// Reduce noise with a kernel 3x3
blur( src_gray, detected_edges, Size(3,3) );
/// Canny detector
Canny( detected_edges, detected_edges, lowThreshold, lowThreshold*ratio, kernel_size );
dst = Scalar::all(0);
src.copyTo( dst, detected_edges);
imshow( window_name, dst );
if(lowThreshold == 0){
imwrite("canny_0.png",dst);
}
if(lowThreshold==50){
imwrite("canny_50.png",dst);
}
if(lowThreshold==100){
imwrite("canny_100.png",dst);
}
}
int main( )
{
src = imread( "/home/qingyuanxingsi/workspace/C++/contents/lufei.jpg" );
if( !src.data )
{ return -1; }
dst.create( src.size(), src.type() );
cvtColor( src, src_gray, CV_BGR2GRAY );
namedWindow( window_name, CV_WINDOW_AUTOSIZE );
createTrackbar( "Min Threshold:", window_name, &lowThreshold, max_lowThreshold, CannyThreshold );
CannyThreshold(0, 0);
waitKey(0);
return 0;
}
通过设定不同的阈值,我们分别得到不同的边缘检测结果:

当我们把阈值均设置为0时,我们得到的是原图像的边缘阵列;
以下分别当低阈值分别设置为50和100时的结果:


TODO BOARD:
- Sobel算子$G_x$,$G_y$定义确认;