计算机视觉(III):霍夫变换直线检测
霍夫变换直线检测基本原理
Hough变换是图像处理中从图像中识别几何形状的基本方法之一,即它可以检测已知形状的目标,而且受噪声和曲线间断的影响小。 Hough变换的基本思想是利用点-线的对偶性。如下图所示:
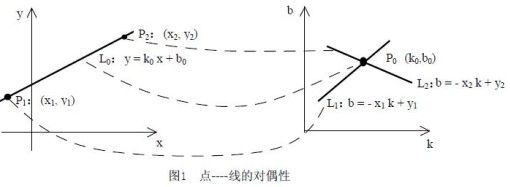
从上图中可看出,$x-y$坐标和$k-b$坐标有点-线的对偶性。$x-y$坐标中的点$P_1$、$P_2$对应于$k-b$坐标中的$L_1、L_2$;而$k-b$坐标中的点$P_0$对应于$x-y$坐标中的线$L_0$。
由于$x-y$坐标中的垂直线的$k$值为无穷大,给计算带来不便,故使用极坐标变换解决这一问题。直角坐标$X-Y$中的一点$(x,y)$,经过极坐标变换为:
\begin{equation} \rho = x * cos \theta + y * sin \theta \end{equation}
在极坐标$\theta-\rho$中变为一条正弦曲线,$\theta$取(0-180°)。可以证明,直角坐标$X-Y$中直线上的点经过Hough变换后,它们的正弦曲线在极坐标$\theta-\rho$有一个公共交点,如下图所示。
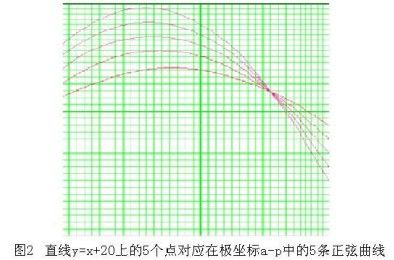
也就是说,极坐标$\theta-\rho$上的一点$(\theta,\rho)$,对应于直角坐标$X-Y$中的一条直线,而且它们是一一对应的。为了检测出直角坐标$X-Y$中由点所构成的直线,可以将极坐标$\theta-\rho$量化成许多小格。根据直角坐标中每个点的坐标$(x,y)$,在$\theta = 0-180°$内以小格的步长计算各个$\rho$值,所得值落在某个小格内,便使该小格的累加记数器加1。当直角坐标中全部的点都变换后,对小格进行检验,计数值最大的小格,其$(\theta,\rho)$值对应于直角坐标中所求直线。
代码示例
以下我们给出一个使用OpenCV检测直线的代码示例:
#include <iostream>
#include "opencv2/core/core.hpp"
#include "opencv2/highgui/highgui.hpp"
#include "opencv2/imgproc/imgproc.hpp"
using namespace std;
using namespace cv;
int main(int argc, char** argv)
{
Mat src = imread("/home/qingyuanxingsi/workspace/C++/contents/jinmen.jpg");
if(src.empty())
{
cout << "can not open the image" << endl;
return -1;
}
Mat dst, cdst;
//Canny operator retrieve edges
Canny(src, dst, 50, 200, 3);
cvtColor(dst, cdst, CV_GRAY2BGR);
vector<Vec4i> lines;
//Probablistic Hough Transformation
HoughLinesP(dst, lines, 1, CV_PI/180, 50, 50, 10 );
for( size_t i = 0; i < lines.size(); i++ )
{
Vec4i l = lines[i];
line(cdst, Point(l[0], l[1]), Point(l[2], l[3]), Scalar(255,0,0), 2, CV_AA);
}
imshow("source", src);
imshow("detected lines", cdst);
imwrite("line.jpg",cdst);
waitKey();
return 0;
}
原图使用金门大桥图片,如下:

检测到的直线图像如下图所示:
