其实本来没准备看Deep Learning的,之前这个高端大气上档次的内容一直都不再我的学习计划之内。基于如下几个原因吧,最后决定还是稍微看一下吧:

• Deep Learning是Machine Learning:A Probabilistic Perspective的最后一章,反正终归是要看的。(之前觉得自己可能看不懂,但是好歹试试水吧);
• 一个小伙伴毕业设计就在做Deep Learning;
• 实验室老大好像对Deep Learning很感兴趣;
• 好奇心害死人啊！！！！！！

言归正传,作为Deep Learning系列的第一篇,我们首先还是说明一下两件事:Deep Learning是什么?Deep Learning是用来干什么的?

A Brief Introduction to Deep Learning

---

背景

机器学习（Machine Learning)是一门专门研究计算机怎样模拟或实现人类的学习行为，以获取新的知识或技能，重新组织已有的知识结构使之不断改善自身的性能的学科。机器能否像人类一样能具有学习能力呢？1959年美国的塞缪尔(Samuel)设计了一个下棋程序，这个程序具有学习能力，它可以在不断的对弈中改善自己的棋艺。4年后，这个程序战胜了设计者本人。又过了3年，这个程序战胜了美国一个保持8年之久的常胜不败的冠军。这个程序向人们展示了机器学习的能力，提出了许多令人深思的社会问题与哲学问题（呵呵，人工智能正常的轨道没有很大的发展，这些什么哲学伦理啊倒发展的挺快。什么未来机器越来越像人，人越来越像机器啊。什么机器会反人类啊，ATM是开第一枪的啊等等。人类的思维无穷啊）。

机器学习虽然发展了几十年，但还是存在很多没有良好解决的问题：

例如图像识别、语音识别、自然语言理解、天气预测、基因表达、内容推荐等等。目前我们通过机器学习去解决这些问题的思路都是这样的（以视觉感知为例子）：

从开始的通过传感器（例如CMOS）来获得数据。然后经过预处理、特征提取、特征选择，再到推理、预测或者识别。最后一个部分，也就是机器学习的部分，绝大部分的工作是在这方面做的，也存在很多的paper和研究。

而中间的三部分，概括起来就是特征表达。良好的特征表达，对最终算法的准确性起了非常关键的作用，而且系统主要的计算和测试工作都耗在这一大部分。但，这块实际中一般都是人工完成的。靠人工提取特征。

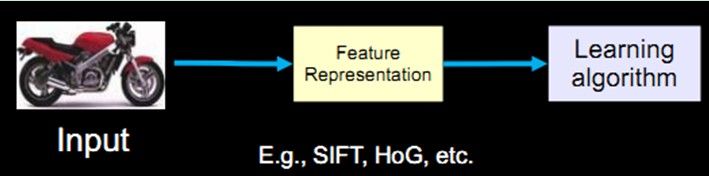
截止现在，也出现了不少NB的特征（好的特征应具有不变性（大小、尺度和旋转等）和可区分性）：例如Sift的出现，是局部图像特征描述子研究领域一项里程碑式的工作。由于SIFT对尺度、旋转以及一定视角和光照变化等图像变化都具有不变性，并且SIFT具有很强的可区分性，的确让很多问题的解决变为可能。但它也不是万能的。

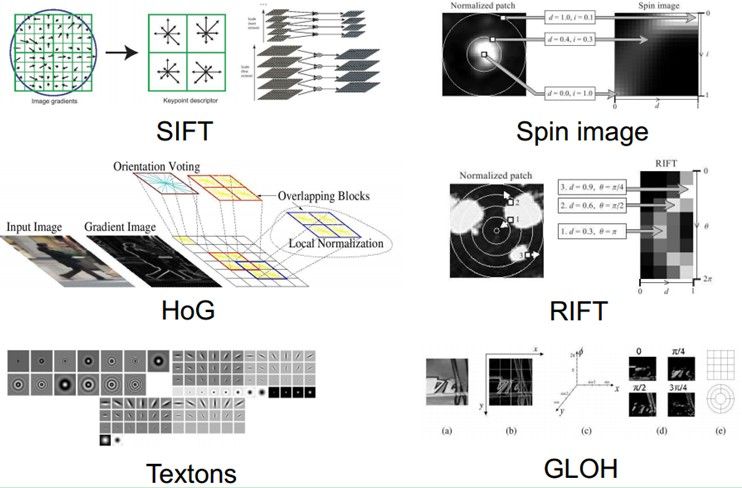
然而，手工地选取特征是一件非常费力、启发式（需要专业知识）的方法，能不能选取好很大程度上靠经验和运气，而且它的调节需要大量的时间。既然手工选取特征不太好，那么能不能自动地学习一些特征呢？答案是能！Deep Learning就是用来干这个事情的，看它的一个别名Unsupervised Feature Learning,就可以顾名思义了，Unsupervised的意思就是不要人参与特征的选取过程。

那它是怎么学习的呢？怎么知道哪些特征好哪些不好呢？我们说机器学习是一门专门研究计算机怎样模拟或实现人类的学习行为的学科。好，那我们人的视觉系统是怎么工作的呢？为什么在茫茫人海，芸芸众生，滚滚红尘中我们都可以找到另一个她（因为，你存在我深深的脑海里，我的梦里 我的心里 我的歌声里……）。人脑那么NB，我们能不能参考人脑，模拟人脑呢？（好像和人脑扯上点关系的特征啊，算法啊，都不错，但不知道是不是人为强加的，为了使自己的作品变得神圣和高雅。）

近几十年以来，认知神经科学、生物学等等学科的发展，让我们对自己这个神秘的而又神奇的大脑不再那么的陌生。也给人工智能的发展推波助澜。

人脑视觉机理

1981 年的诺贝尔医学奖，颁发给了David Hubel（出生于加拿大的美国神经生物学家)和TorstenWiesel，以及Roger Sperry。前两位的主要贡献，是发现了视觉系统的信息处理过程是分级的：

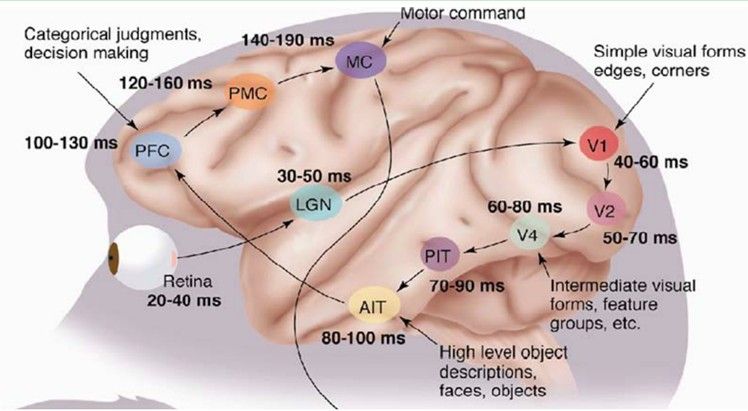
我们看看他们做了什么。1958 年，DavidHubel 和Torsten Wiesel在JohnHopkins University，研究瞳孔区域与大脑皮层神经元的对应关系。他们在猫的后脑头骨上，开了一个3毫米的小洞，向洞里插入电极，测量神经元的活跃程度。

然后，他们在小猫的眼前，展现各种形状、各种亮度的物体。并且，在展现每一件物体时，还改变物体放置的位置和角度。他们期望通过这个办法，让小猫瞳孔感受不同类型、不同强弱的刺激。

之所以做这个试验，目的是去证明一个猜测。位于后脑皮层的不同视觉神经元，与瞳孔所受刺激之间，存在某种对应关系。一旦瞳孔受到某一种刺激，后脑皮层的某一部分神经元就会活跃。经历了很多天反复的枯燥的试验，同时牺牲了若干只可怜的小猫，David Hubel 和Torsten Wiesel发现了一种被称为“方向选择性细胞（Orientation Selective Cell）”的神经元细胞。当瞳孔发现了眼前的物体的边缘，而且这个边缘指向某个方向时，这种神经元细胞就会活跃。

这个发现激发了人们对于神经系统的进一步思考。神经-中枢-大脑的工作过程，或许是一个不断迭代、不断抽象的过程。

这里的关键词有两个，一个是抽象，一个是迭代。从原始信号，做低级抽象，逐渐向高级抽象迭代。人类的逻辑思维，经常使用高度抽象的概念。

例如，从原始信号摄入开始（瞳孔摄入像素Pixels），接着做初步处理（大脑皮层某些细胞发现边缘和方向），然后抽象（大脑判定，眼前的物体的形状，是圆形的），然后进一步抽象（大脑进一步判定该物体是只气球）。

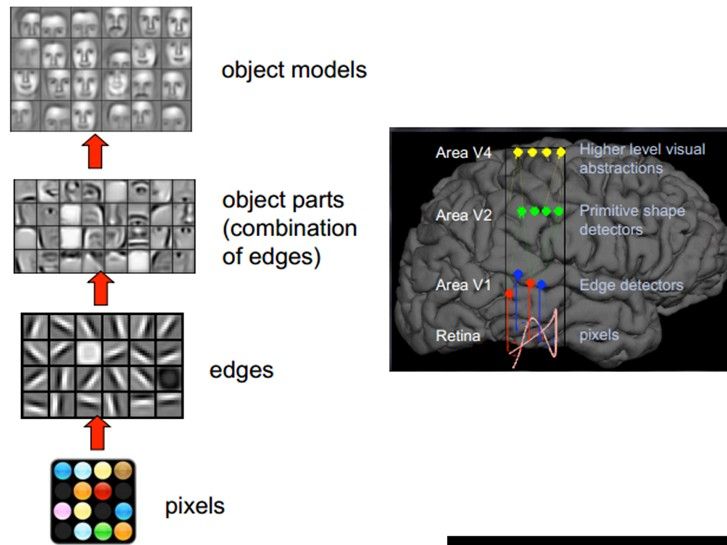
这个生理学的发现，促成了计算机人工智能，在四十年后的突破性发展。

总的来说，人的视觉系统的信息处理是分级的。从低级的V1区提取边缘特征，再到V2区的形状或者目标的部分等，再到更高层，整个目标、目标的行为等。也就是说高层的特征是低层特征的组合，从低层到高层的特征表示越来越抽象，越来越能表现语义或者意图。而抽象层面越高，存在的可能猜测就越少，就越利于分类。例如，单词集合和句子的对应是多对一的，句子和语义的对应又是多对一的，语义和意图的对应还是多对一的，这是个层级体系。

敏感的人注意到关键词了：分层。而Deep learning的Deep是不是就表示存在多少层，也就是多深呢？没错。那Deep Learning是如何借鉴这个过程的呢？毕竟是归于计算机来处理，面对的一个问题就是怎么对这个过程建模？

因为我们要学习的是特征的表达，那么关于特征，或者说关于这个层级特征，我们需要了解地更深入点。所以在说Deep Learning之前，我们有必要再啰嗦下特征。

特征

特征是机器学习系统的原材料，对最终模型的影响是毋庸置疑的。如果数据被很好的表达成了特征，通常线性模型就能达到满意的精度。那对于特征，我们需要考虑什么呢？

特征表示的粒度

学习算法在一个什么粒度上的特征表示，才有能发挥作用？就一个图片来说，像素级的特征根本没有价值。例如下面的摩托车，从像素级别，根本得不到任何信息，其无法进行摩托车和非摩托车的区分。而如果特征是一个具有结构性（或者说有含义）的时候，比如是否具有车把手（handle），是否具有车轮（wheel），就很容易把摩托车和非摩托车区分，学习算法才能发挥作用。

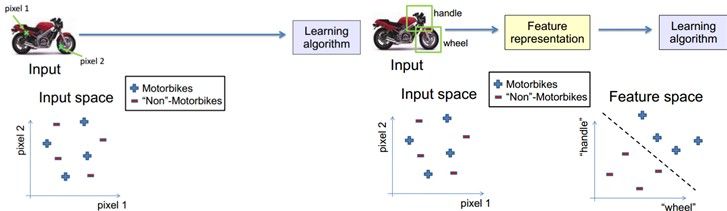
初级(浅层)特征表示

既然像素级的特征表示方法没有作用，那怎样的表示才有用呢？

1995 年前后，Bruno Olshausen和 David Field 两位学者任职Cornell University，他们试图同时用生理学和计算机的手段，双管齐下，研究视觉问题。

他们收集了很多黑白风景照片，从这些照片中，提取出400个小碎片，每个照片碎片的尺寸均为16x16像素，不妨把这400个碎片标记为$S[i]$,$i= 0,.. 399$。接下来，再从这些黑白风景照片中，随机提取另一个碎片，尺寸也是 16x16 像素，不妨把这个碎片标记为$T$。

他们提出的问题是，如何从这400个碎片中，选取一组碎片$S[k]$,通过叠加的办法，合成出一个新的碎片，而这个新的碎片，应当与随机选择的目标碎片$T$尽可能相似，同时$S[k]$的数量尽可能少。用数学的语言来描述，就是：

\begin{equation} \sum_k (a[k] * S[k]) \rightarrow T \end{equation}

其中$a[k]$是在叠加碎片$S[k]$时的权重系数。

为解决这个问题，Bruno Olshausen和 David Field发明了一个算法：稀疏编码(Sparse Coding)。

稀疏编码是一个重复迭代的过程，每次迭代分两步:

1. 选择一组$S[k]$，然后调整$a[k]$，使得$\sum_k (a[k]*S[k])$最接近$T$;
2. 固定住$a[k]$,在400个碎片中,选择其它更合适的碎片$S\prime[k]$，替代原先的$S[k]$,使得$\sum_k (a[k]*S\prime[k])$最接近$T$。

经过几次迭代后，最佳的$S[k]$组合，被遴选出来了。令人惊奇的是，被选中的$S[k]$,基本上都是照片上不同物体的边缘线，这些线段形状相似，区别在于方向。

Bruno Olshausen和 David Field的算法结果，与David Hubel 和Torsten Wiesel的生理发现，不谋而合！

也就是说，复杂图形，往往由一些基本结构组成。比如下图：一个图可以通过用64种正交的edges（可以理解成正交的基本结构）来线性表示。比如样例$x$可以用1-64个edges中的三个按照0.8,0.3,0.5的权重调和而成。而其他基本edge没有贡献，因此均为0 。

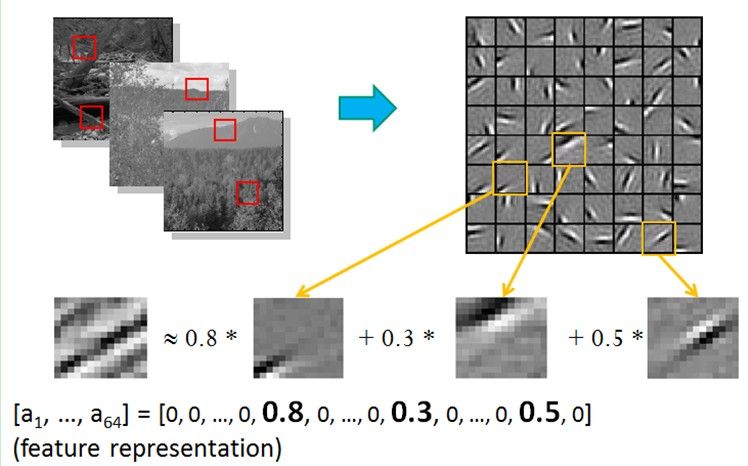
另外，大牛们还发现，不仅图像存在这个规律，声音也存在。他们从未标注的声音中发现了20种基本的声音结构，其余的声音可以由这20种基本结构合成。

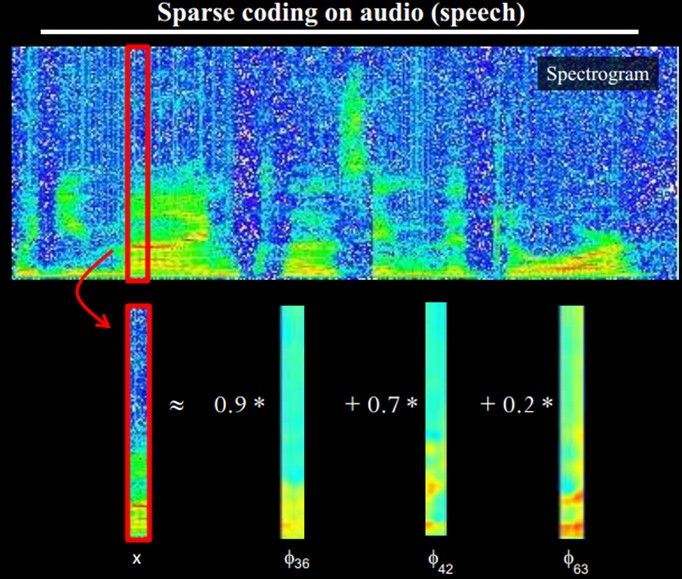
结构性特征表示

小块的图形可以由基本edge构成，更结构化，更复杂的，具有概念性的图形如何表示呢？这就需要更高层次的特征表示，比如V2，V4。因此V1看像素级是像素级。V2看V1是像素级，这个是层次递进的，高层表达由底层表达的组合而成。专业点说就是基basis。V1提取出的basis是边缘，然后V2层是V1层这些basis的组合，这时候V2区得到的又是高一层的basis。即上一层的basis组合的结果，上上层又是上一层的组合basis(所以有大牛说Deep learning就是“搞基”，因为难听，所以美其名曰Deep learning或者Unsupervised Feature Learning）。

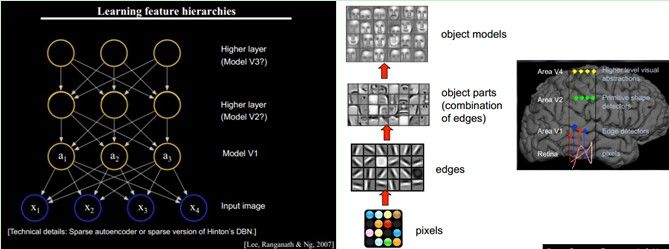
直观上说，就是找到make sense的小patch再将其进行combine，就得到了上一层的feature，递归地向上learning feature。

在不同object上做training所得的edge basis是非常相似的，但object parts和models就会completely different了（那咱们分辨car或者face是不是容易多了):

从文本来说，一个doc表示什么意思？我们描述一件事情，用什么来表示比较合适？用一个一个字嘛，我看不是，字就是像素级别了，起码应该是term，换句话说每个doc都由term构成，但这样表示概念的能力就够了嘛，可能也不够，需要再上一步，达到topic级，有了topic，再到doc就合理。但每个层次的数量差距很大，比如doc表示的概念->topic（千-万量级)->term（10万量级)->word（百万量级）。

一个人在看一个doc的时候，眼睛看到的是word，由这些word在大脑里自动切词形成term，在按照概念组织的方式，先验的学习，得到topic，然后再进行高层次的learning。

需要有多少个特征？

我们知道需要层次的特征构建，由浅入深，但每一层该有多少个特征呢？

任何一种方法，特征越多，给出的参考信息就越多，准确性会得到提升。但特征多意味着计算复杂，探索的空间大，可以用来训练的数据在每个特征上就会稀疏，都会带来各种问题，并不一定特征越多越好。

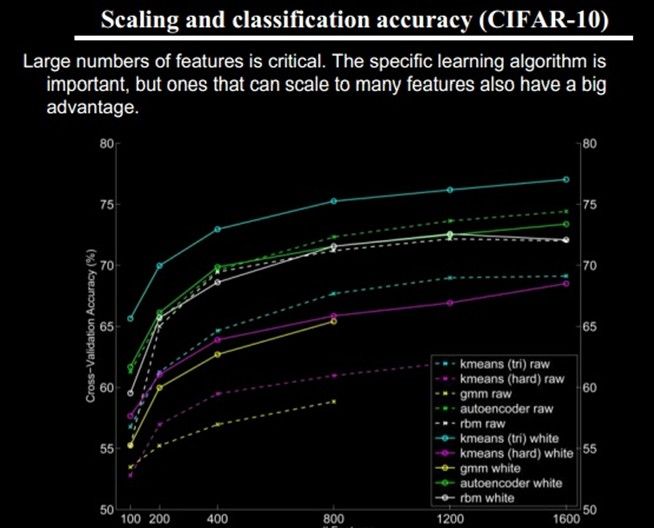
好了，到了这一步，终于可以聊到Deep Learning了。上面我们聊到为什么会有Deep Learning（让机器自动学习良好的特征，而免去人工选取过程。还有参考人的分层视觉处理系统），我们得到一个结论就是Deep Learning需要多层来获得更抽象的特征表达。那么多少层才合适呢？用什么架构来建模呢？怎么进行非监督训练呢？以下我们给出Deep Learning的基本思想。

Deep Learning的基本思想

假设我们有一个系统$S$，它有$n$层$(S_1,…S_n)$，它的输入是$I$，输出是$O$，形象地表示为:$I \rightarrow S_1 \rightarrow S_2 \rightarrow ….\rightarrow S_n \rightarrow O$，如果输出$O$等于输入$I$，即输入$I$经过这个系统变化之后没有任何的信息损失(呵呵，大牛说，这是不可能的。信息论中有个“信息逐层丢失”的说法（信息处理不等式):设处理$a$信息得到$b$，再对$b$处理得到$c$，那么可以证明：$a$和$c$的互信息不会超过$a$和$b$的互信息。这表明信息处理不会增加信息，大部分处理会丢失信息。当然了，如果丢掉的是没用的信息那多好啊），保持了不变，这意味着输入$I$经过每一层$S_i$都没有任何的信息损失，即在任何一层$S_i$，它都是原有信息（即输入$I$）的另外一种表示。现在回到我们的主题Deep Learning，我们需要自动地学习特征，假设我们有一堆输入$I$(如一堆图像或者文本),假设我们设计了一个系统$S$（有$n$层），我们通过调整系统中参数，使得它的输出仍然是输入$I$，那么我们就可以自动地获取得到输入$I$的一系列层次特征，即$S_1，…, S_n$。

对于深度学习来说，其思想就是对堆叠多个层，也就是说这一层的输出作为下一层的输入。通过这种方式，就可以实现对输入信息进行分级表达了。

另外，前面是假设输出严格地等于输入，这个限制太严格，我们可以略微地放松这个限制，例如我们只要使得输入与输出的差别尽可能地小即可，这个放松会导致另外一类不同的Deep Learning方法。上述就是Deep Learning的基本思想。

BP Neural Network

---

上述我们主要意在建立关于Deep Learning一点直观的印象,下面我们就开始介绍Deep Learning所涉及的模型了。首先第一个要介绍的就是Sparse AutoEncoder(稀疏自编码器)。为了更好的理解Sparse AutoEncoder,我们首先介绍一下Back Propagation Algorithm,而采用Back Propagation算法的一个典型的代表就是BP神经网络(想了解神经网络基础知识的童鞋请自行Google之)。以下我们便主要介绍BP神经网络。

概述

BP(Back Propagation)神经网络是1986年由Rumelhart和McCelland为首的科研小组提出，参见他们发表在Nature上的论文Learning representations by back-propagating errors.值得一提的是，该文的第三作者Geoffrey E. Hinton就是在深度学习邻域率先取得突破的神犇。

BP神经网络是一种按误差逆向传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP网络能学习和存贮大量的 输入-输出模式映射关系，而无需事前揭示描述这种映射关系的数学方程。它的学习规则是使用最速下降法，通过反向传播来不断 调整网络的权值和阈值，使网络的误差平方和最小。

其中,前馈是指输入从输入层到隐含层到输出层前向传播,而误差则由输出层反向经隐含层传到输入层,而在误差反向传播的过程中动态更新神经网络连接权值,以使得网络的误差平方和最小。

BP网络模型

一个典型的BP神经网络模型如下图所示。

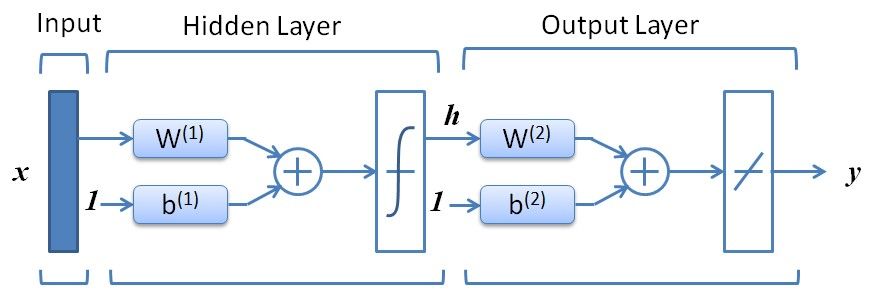
BP神经网络与其他神经网络模型类似，不同的是，BP神经元的传输函数为非线性函数(而在感知机中为阶跃函数，在线性神经网络中为线性函数)，最常用的是log-sigmoid函数或tan-sigmoid函数。BP神经网络(BPNN)一般为多层神经网络，上图中所示的BP神经网络的隐层的传输函数即为非线性函数，隐层可以有多层，而输出层的传输函数为线性函数，当然也可以是非线性函数，只不过线性函数的输出结果取值范围较大，而非线性函数则限制在较小范围（如logsig函数输出 取值在(0,1)区间）。上图所示的神经网络的输入输出关系如下：

• 输入层与隐层的关系:

\begin{equation} \boldsymbol{h} = \mathit{f_{1}} (\boldsymbol{W^{(1)}x}+\boldsymbol{b^{(1)}}) \end{equation}

其中$x$为$m$维特征向量(列向量)，$\boldsymbol{W^{(1)}}$为$n×m$维权值矩阵，$\boldsymbol{b^{(1)}}$为$n$维的偏置(bias)向量(列向量)。

• 隐层与输出层的关系:

\begin{equation} \boldsymbol{y} = \mathit{f_{2}} (\boldsymbol{W^{(2)}h}+\boldsymbol{b^{(2)}}) \end{equation}

BP网络的学习方法

神经网络的关键之一是权值的确定，也即神经网络的学习，下面主要讨论一下BP神经网络的学习方法，它是一种监督学习的方法。

假定我们有$q$个带label的样本(即输入)$p_1,p_2,…,p_q$，对应的label(即期望输出Target)为$T_1,T_2,…,T_q$，神经网络的实际输出为$a2_1,a2_2,…,a2_q$，隐层的输出为$a1[.]$.那么可以定义误差函数：

\begin{equation} \boldsymbol{E(W,B)} = \frac{1}{2}\sum_{k=1}^{n}(t_{k} - a2_{k})^{2} \end{equation}

BP算法的目标是使得实际输出approximate期望输出，即使得训练误差最小化。BP算法利用梯度下降(Gradient Descent)法来求权值的变化及误差的反向传播。对于上图中的BP神经网络，我们首先计算输出层的权值的变化量，从第$i$个输入到第$k$个输出的权值改变为:

\begin{equation} \begin{split} \Delta w2_{ki} &= - \eta \frac{\partial E}{\partial w2_{ki}} \\ &= - \eta \frac{\partial E}{\partial a2_{k}} \frac{\partial a2_{k}}{\partial w2_{ki}} \\ &= \eta (t_{k}-a2_{k})f_{2}’a1_{i} \\ &= \eta \delta_{ki}a1_{i} \end{split} \end{equation}

其中$\eta$为学习速率。同理可得:

\begin{equation} \begin{split} \Delta b2_{ki} &= - \eta \frac{\partial E}{\partial b2_{ki}} \\ &= - \eta \frac{\partial E}{\partial a2_{k}} \frac{\partial a2_{k}}{\partial b2_{ki}} \\ &= \eta (t_{k}-a2_{k})f_{2}’ \\ &= \eta \delta_{ki} \end{split} \end{equation}

而隐层的权值变化为:

\begin{equation} \begin{split} \Delta w1_{ij} &= - \eta \frac{\partial E}{\partial w1_{ij}} \\ &= - \eta \frac{\partial E}{\partial a2_{k}} \frac{\partial a2_{k}}{\partial a1_{i}} \frac{\partial a1_{i}}{\partial w1_{ij}} \\ &= \eta \sum_{k=1}^{n}(t_{k}-a2_{k})f_{2}’w2_{ki}f_{1}’p_{j} \\ &= \eta \delta_{ij}p_{j} \end{split} \end{equation}

其中，$\delta_{ij} = e_{i}f_{1}’, e_{i} = \sum_{k=1}^{n}\delta_{ki}w2_{ki}$。同理可得，$\Delta b1_{i} = \eta \delta_{ij}$。

这里我们注意到，输出层的误差为$e_j,j=1..n$，隐层的误差为$e_i,i=1..m$，其中$e_i$可以认为是$e_j$的加权组合，由于作用函数的 存在，$e_j$的等效作用为$\delta_{ji} = e_{j}f’()$。

BP网络的设计

在进行BP网络的设计是，一般应从网络的层数、每层中的神经元个数和激活函数、初始值以及学习速率等几个方面来进行考虑，下面是一些选取的原则。

• 网络的层数

理论已经证明，具有偏差和至少一个S型隐层加上一个线性输出层的网络，能够逼近任何有理函数，增加层数可以进一步降低误差，提高精度，但同时也是网络 复杂化。另外不能用仅具有非线性激活函数的单层网络来解决问题，因为能用单层网络解决的问题，用自适应线性网络也一定能解决，而且自适应线性网络的 运算速度更快，而对于只能用非线性函数解决的问题，单层精度又不够高，也只有增加层数才能达到期望的结果。

• 隐层神经元的个数

网络训练精度的提高，可以通过采用一个隐含层，而增加其神经元个数的方法来获得，这在结构实现上要比增加网络层数简单得多。一般而言，我们用精度和 训练网络的时间来恒量一个神经网络设计的好坏：

1. 神经元数太少时，网络不能很好的学习，训练迭代的次数也比较多，训练精度也不高。

2. 神经元数太多时，网络的功能越强大，精确度也更高，训练迭代的次数也大，可能会出现过拟合(over fitting)现象。 由此，我们得到神经网络隐层神经元个数的选取原则是：在能够解决问题的前提下，再加上一两个神经元，以加快误差下降速度即可。

3. 初始权值的选取 一般初始权值是取值在$(−1,1)$之间的随机数。另外威得罗等人在分析了两层网络是如何对一个函数进行训练后，提出选择初始权值量级为$\sqrt[r]{s}$的策略， 其中$r$为输入个数，$s$为第一层神经元个数。

4. 学习速率 学习速率一般选取为0.01−0.8，大的学习速率可能导致系统的不稳定，但小的学习速率导致收敛太慢，需要较长的训练时间。对于较复杂的网络， 在误差曲面的不同位置可能需要不同的学习速率，为了减少寻找学习速率的训练次数及时间，比较合适的方法是采用变化的自适应学习速率，使网络在 不同的阶段设置不同大小的学习速率。

5. 期望误差的选取 在设计网络的过程中，期望误差值也应当通过对比训练后确定一个合适的值，这个合适的值是相对于所需要的隐层节点数来确定的。一般情况下，可以同时对两个不同 的期望误差值的网络进行训练，最后通过综合因素来确定其中一个网络。

BP网络的局限性

BP网络具有以下的几个问题：

1. 需要较长的训练时间：这主要是由于学习速率太小所造成的，可采用变化的或自适应的学习速率来加以改进。
2. 完全不能训练：这主要表现在网络的麻痹上，通常为了避免这种情况的产生，一是选取较小的初始权值，而是采用较小的学习速率。
3. 局部最小值：这里采用的梯度下降法可能收敛到局部最小值，采用多层网络或较多的神经元，有可能得到更好的结果。

BP网络的改进

BP算法改进的主要目标是加快训练速度，避免陷入局部极小值等，常见的改进方法有带动量因子算法、自适应学习速率、变化的学习速率以及作用函数后缩法等。 动量因子法的基本思想是在反向传播的基础上，在每一个权值的变化上加上一项正比于前次权值变化的值，并根据反向传播法来产生新的权值变化。而自适应学习速率的方法则是针对一些特定的问题的。改变学习速率的方法的原则是，若连续几次迭代中，若目标函数对某个权倒数的符号相同，则这个权的学习速率增加，反之若符号相反则减小它的学习速率。而作用函数后缩法则是将作用函数进行平移，即加上一个常数。

Sparse AutoEncoder

---

有了以上基础知识,我们以下介绍一下Sparse AutoEncoder(稀疏自编码器)。

目前为止，我们已经介绍了BP神经网络,而它采用的是有监督学习(使用带标签数据)。现在假设我们只有一个没有带类别标签的训练样本集合 ${x^{(1)}, x^{(2)}, x^{(3)}, \ldots}$，其中$x^{(i)} \in \Re^{n}$.自编码神经网络是一种无监督学习算法，它使用了反向传播算法，并让目标值等于输入值，比如 $y^{(i)} = x^{(i)}$ 。下图是一个自编码神经网络的示例。

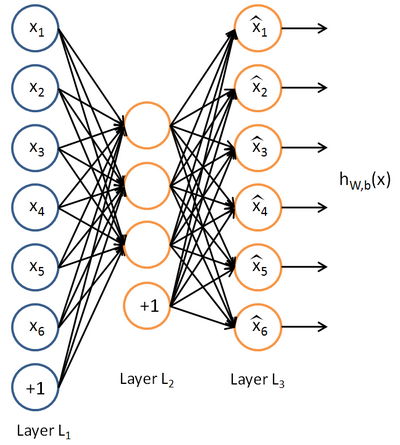
自编码神经网络尝试学习一个$h_{W,b}(x) \approx x$的函数。换句话说，它尝试逼近一个恒等函数，从而使得输出$\hat{x}$接近于输入 $x$ 。恒等函数虽然看上去不太有学习的意义，但是当我们为自编码神经网络加入某些限制，比如限定隐藏神经元的数量，我们就可以从输入数据中发现一些有趣的结构。举例来说，假设某个自编码神经网络的输入$x$是一张$10\times10$图像（共100个像素）的像素灰度值，于是 $n=100$,其隐藏层$L_2$中有50个隐藏神经元。注意，输出也是100维的$y \in \Re^{100}$由于只有50个隐藏神经元，我们迫使自编码神经网络去学习输入数据的压缩表示，也就是说，它必须从50维的隐藏神经元激活度向量$a^{(2)} \in \Re^{50}$中重构出100维的像素灰度值输入$x$。如果网络的输入数据是完全随机的，比如每一个输入$x_i$都是一个跟其它特征完全无关的独立同分布高斯随机变量，那么这一压缩表示将会非常难学习。但是如果输入数据中隐含着一些特定的结构，比如某些输入特征是彼此相关的，那么这一算法就可以发现输入数据中的这些相关性。事实上，这一简单的自编码神经网络通常可以学习出一个跟主元分析（PCA）结果非常相似的输入数据的低维表示。

我们刚才的论述是基于隐藏神经元数量较小的假设。但是即使隐藏神经元的数量较大（可能比输入像素的个数还要多），我们仍然通过给自编码神经网络施加一些其他的限制条件来发现输入数据中的结构。具体来说，如果我们给隐藏神经元加入稀疏性限制，那么自编码神经网络即使在隐藏神经元数量较多的情况下仍然可以发现输入数据中一些有趣的结构。

稀疏性可以被简单地解释如下。如果当神经元的输出接近于1的时候我们认为它被激活，而输出接近于0的时候认为它被抑制，那么使得神经元大部分的时间都是被抑制的限制则被称作稀疏性限制。这里我们假设的神经元的激活函数是sigmoid函数。如果你使用tanh作为激活函数的话，当神经元输出为-1的时候，我们认为神经元是被抑制的。

注意到$a^{(2)}_j$表示隐藏神经元$j$的激活度，但是这一表示方法中并未明确指出哪一个输入$x$带来了这一激活度。所以我们将使用 $a^{(2)}_j(x)$来表示在给定输入为$x$情况下，自编码神经网络隐藏神经元$j$的激活度。 进一步，让

\begin{equation} \hat\rho_j = \frac{1}{m} \sum_{i=1}^m \left[ a^{(2)}_j(x^{(i)}) \right] \end{equation}

表示隐藏神经元$j$的平均活跃度（在训练集上取平均）。我们可以近似的加入一条限制

\begin{equation} \hat\rho_j = \rho, \end{equation}

其中，$\rho$是稀疏性参数，通常是一个接近于0的较小的值（比如$\rho=0.05$）。换句话说，我们想要让隐藏神经元$j$的平均活跃度接近0.05。为了满足这一条件，隐藏神经元的活跃度必须接近于0。

为了实现这一限制，我们将会在我们的优化目标函数中加入一个额外的惩罚因子，而这一惩罚因子将惩罚那些$\hat\rho_j$和$\rho$有显著不同的情况从而使得隐藏神经元的平均活跃度保持在较小范围内。惩罚因子的具体形式有很多种合理的选择，我们将会选择以下这一种：

\begin{equation} \sum_{j=1}^{s_2} \rho \log \frac{\rho}{\hat\rho_j} + (1-\rho) \log \frac{1-\rho}{1-\hat\rho_j}. \end{equation}

这里，$s_2$是隐藏层中隐藏神经元的数量，而索引$j$依次代表隐藏层中的每一个神经元。如果你对相对熵(KL divergence）比较熟悉，这一惩罚因子实际上是基于它的。于是惩罚因子也可以被表示为:

\begin{equation} \sum_{j=1}^{s_2} {\rm KL}(\rho || \hat\rho_j), \end{equation}

其中 ${\rm KL}(\rho || \hat\rho_j)= \rho \log \frac{\rho}{\hat\rho_j} + (1-\rho) \log \frac{1-\rho}{1-\hat\rho_j}$是一个以 $\rho$为均值和一个以$\hat\rho_j$为均值的两个伯努利随机变量之间的相对熵。相对熵是一种标准的用来测量两个分布之间差异的方法。

这一惩罚因子有如下性质，当$\hat\rho_j = \rho$时,$\textstyle {\rm KL}(\rho || \hat\rho_j) = 0$，并且随着$\hat\rho_j$与$\rho$ 之间的差异增大而单调递增。举例来说，在下图中，我们设定$\rho = 0.2$并且画出了相对熵值${\rm KL}(\rho || \hat\rho_j)$随着 $\hat\rho_j$变化的变化。

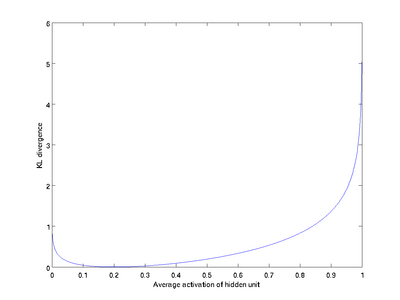
我们可以看出，相对熵在$\hat\rho_j=\rho$时达到它的最小值0，而当$\hat\rho_j$靠近0或者1的时候，相对熵则变得非常大（其实是趋向于$\infty$）。所以，最小化这一惩罚因子具有使得$\hat\rho_j$靠近$\rho$的效果。现在，我们的总体代价函数可以表示为:

\begin{equation} J_{\rm sparse}(W,b) = J(W,b) + \beta \sum_{j=1}^{s_2} {\rm KL}(\rho || \hat\rho_j), \end{equation} 其中$J(W,b)$如之前所定义，而$\beta$控制稀疏性惩罚因子的权重。$\hat\rho_j$项则也（间接地）取决于$W,b$,因为它是隐藏神经元$j$的平均激活度，而隐藏层神经元的激活度取决于$W,b$。

总而言之,通过控制隐含层神经元的数量或对它们施加稀疏性限制,我们就能得到关于原始数据的一种有效的特征表示。具体而言,当我们采用我们上面提到的2D图像作为输入时,不同的隐藏单元学会了在图像的不同位置和方向进行边缘检测。显而易见，这些特征对物体识别等计算机视觉任务是十分有用的。若将其用于其他输入域（如音频），该算法也可学到对这些输入域有用的表示或特征。

参考文献

---

1. Deep Learning（深度学习）学习笔记整理系列之（一)
2. Deep Learning（深度学习）学习笔记整理系列之（二)
3. Deep Learning（深度学习）学习笔记整理系列之（三)
4. 反向传播(BP)神经网络
5. BP神经网络模型与学习算法
6. BP神经网络C++实现
7. 自稀疏算法与稀疏性
8. 可视化自编码器训练结果

Comment

---