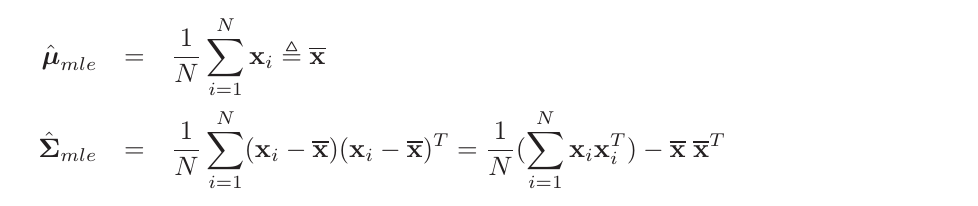六 15 三月 2014

Filed under Machine Learning

Tags Machine Learning Gaussian Models Generative Models

在上一篇中我们着重介绍了对于离散数据的生成模型，紧接上一篇，本篇我们介绍对于连续数据的生成模型。好吧,废话我们就不多说了,直接进入正文。

MLE for MVN

---

Basics about MVN

谈到连续分布,我们很自然地就会想到高斯分布,从小学到现在，印象中第一个走入我脑海中的看着比较高端大气上档次的就是Gaussian分布了。这次我们的重点也会完全集中在Gaussian分布之了,在正式讨论之前，我们先介绍一些关于Gaussian分布的基础知识。

在$D$维空间中,MVN(Multivariate Normal)多变量正态分布的概率分布函数具有如下形式:

\begin{equation} N(x|\mu,\Sigma) \triangleq \frac{1}{(2\pi)^{D/2}det(\Sigma)^{1/2}} exp[-\frac{1}{2}(x-\mu)^T\Sigma^{-1}(x-\mu)] \end{equation}

上式中的指数部分是$x$与$\mu$之间的Mahalanobis距离。为了更好地理解这个量,我们对$\Sigma$做特征值分解,即$\Sigma = U \Lambda U^T$,其中$U$是一正交阵,满足$U^TU=I$,而$\Lambda$是特征值矩阵。

通过特征值分解,我们有:

\begin{equation} \Sigma^{-1} = U^{-T}\Lambda^{-1}U^{-1} = U\Lambda^{-1}U^T = \sum_{i=1}^{D}\frac{1}{\lambda_i}u_iu_i^T \end{equation}

其中,$u_i$是$U$的第$i$列。因此Mahalanobis距离可被改写为:

\begin{equation} \begin{split} (x-\mu)^T\Sigma^{-1}(x-\mu) &= (x-\mu)^T (\sum_{i=1}^{D}\frac{1}{\lambda_i}u_iu_i^T) (x-\mu) \\ &= \sum_{i=1}^{D} \frac{1}{\lambda_i}(x-\mu)^T u_iu_i^T (x-\mu) \\ &= \sum_{i=1}^{D} \frac{y_i^2}{x_i} \\ \end{split} \end{equation}

其中,$y_i \triangleq u_i^T(x-\mu)$。另2维空间中的椭圆方程为:

$$\frac{y_1^2}{\lambda_1} + \frac{y_2^2}{\lambda_2} = 1$$

因此我们可知Gaussian概率密度的等高线沿着椭圆分布,特征向量决定椭圆的朝向,而特征值则决定椭圆有多“椭”。一般来说，如果我们将坐标系移动$\mu$,然后按$U$旋转，此时的欧拉距离即为Mahalanobis距离。

MLE for MVN

以下我们给出MVN参数的MLE(极大似然估计)的证明:

Theorem 3.1 若我们获取的$N$个独立同分布的样本$x_i \sim\ N(x|\mu,\Sigma)$,则关于$\mu$以及 $\Sigma$的极大似然分布如下:

我们不加证明地给出如下公式组:

\begin{equation} \begin{split} &\frac{\partial(b^Ta)}{\partial a} = b \\ &\frac{\partial(a^TAa)}{\partial a} = (A+A^T)a \\ &\frac{\partial}{\partial A} tr(BA) = B^T \\ &\frac{\partial}{\partial A} log |A| = A^{-T} \\ &tr(ABC) = tr(CAB) = tr(BCA) \end{split} \end{equation}

最后一个等式称为迹的循环置换性质(cyclic permutation property)。利用这个性质,我们使用trace trick可以得到下式:

$$x^TAx = tr(x^TAx) = tr(xx^TA) = tr(Axx^T)$$

证明:

对数似然函数为:

\begin{equation} l(\mu,\Sigma) = log p(D|\mu,\Sigma) = \frac{N}{2} log |\Lambda| - \frac{1}{2} \sum_{i=1}^{N} (x_i-\mu)^T \Lambda (x_i-\mu) \end{equation}

其中，$\Lambda = \Sigma^{-1}$为精度矩阵。令$y_i=x_i-\mu$并利用链式法则有:

\begin{equation} \frac{\partial}{\partial \mu}(x_i-\mu)^T \Sigma^{-1} (x_i-\mu) = \frac {\partial}{\partial y_i} y_i^T \Sigma^{-1} y_i \frac{\partial y_i}{\partial \mu}=-(\Sigma^{-T}+\Sigma^{-1})y_i \end{equation}

即:

\begin{equation} \frac{\partial}{\partial \mu} l(\mu,\Sigma) = -\frac{1}{2} \sum_{i=1}^{N} -2\Sigma^{-1}(x_i-\mu) = 0 \end{equation}

故有:

\begin{equation} \hat{\mu} = \frac{1}{N} \sum_{i=1}^{N} x_i = \bar{x} \end{equation}

即最大似然均值即为经验均值。

利用trace trick我们重写对数似然函数为:

\begin{equation} l(\Lambda) = \frac{N}{2} log |\Lambda| - \frac{1}{2} \sum_{i} tr[(x_i-\mu)(x_i-\mu)^T \Lambda] = \frac{N}{2} log |\Lambda| - \frac{1}{2} tr[S_u\Lambda] \end{equation}

其中，$S_u \triangleq \sum_{i=1}^{N} (x_i-\mu)(x_i-\mu)^T$,业界尊称其为分散度矩阵(Scatter Matrix),以后我们聊LDA的时候会再次碰到。对$\Lambda$求偏导有:

\begin{equation} \frac{\partial l(\Lambda)}{\partial \Lambda} = \frac{N}{2}\Lambda^{-T} - \frac{1}{2} S_u^{T} = 0 \end{equation}

得:

\begin{equation} \hat{\Sigma} = \frac{1}{N} \sum_{i=1}^{N} (x_i-\mu)(x_i-\mu)^T \end{equation}

证毕。

Gaussian Discriminant Analysis

---

我们在上一篇中提到了Naive Bayes方法,其实质无非是估计在每一类下特定的样本出现的概率，进而我们可以把该特定样本分配给概率值最大的那个类。而对于连续数据而言，其实质其实也是一样的，每一个MVN(我们可以看做一类或者一个Component)都可能生成一些数据，我们估计在每一个Component下生成特定样本的概率，然后把该特定样本分配给概率值最大的那个Component即可。即我们可以定义如下的条件分布:

\begin{equation} p(x|y=c,\theta) = N(x|\mu_c,\Sigma_c) \end{equation}

上述模型即为高斯判别分析(Gaussian Discriminant Analysis,GDA)(注意,该模型为生成模型，而不是判别模型)。如果$\Sigma_c$是对角阵，即所有的特征都是独立的时，该模型等同于Naive Bayes.

QDA

在上式中带入高斯密度函数的定义，则有:

\begin{equation} p(y=c|x,\theta) = \frac{\pi_c |2\pi\Sigma_c|^{-1 \over 2}exp[-{1 \over 2}(x-\mu_c)^T\Sigma_C^{-1}(x-\mu_c)]}{\sum_{c\prime}\pi_{c\prime} |2\pi\Sigma_{c\prime}|^{-1 \over 2}exp[-{1 \over 2}(x-\mu_{c\prime})^T\Sigma_{c\prime}^{-1}(x-\mu_{c\prime})]} \end{equation}

上式中$\pi$为各个Component的先验概率分布。根据上式得到的模型则称为Quadratic Discriminant Analysis(QDA).以下给出在2类以及3类情形下可能的决策边界形状,如下图所示:

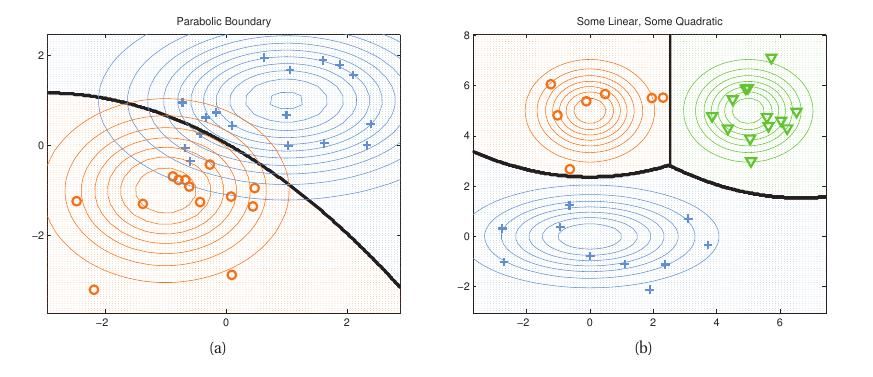
Linear Discriminant Analysis(LDA)

当各个Gaussian Component的协方差矩阵相同时，此时我们有:

\begin{equation} \begin{split} p(y=c|x,\theta) &\propto \pi_c exp[\mu_c^T\Sigma^{-1}x-{1 \over 2}x^T\Sigma^{-1}x-{1 \over 2}\mu_c^T\Sigma^{-1}\mu_c] \\ &= exp[\mu_c^T\Sigma^{-1}x-{1 \over 2}\mu_c^T\Sigma^{-1}\mu_c+log\pi_c]exp[-{1 \over 2}x^T\Sigma^{-1}x] \end{split} \end{equation}

上式中$exp[-{1 \over 2}x^T\Sigma^{-1}x]$是独立于$c$的，分子分母相除抵消到此项。

令:

\begin{equation} \begin{split} \gamma_c &= -{1 \over 2}\mu_c^T\Sigma^{-1}\mu_c+log\pi_c \\ \beta_c &= \Sigma^{-1}\mu_c \end{split} \end{equation}

于是有:

\begin{equation} p(y=c|x,\theta) = \frac{e^{\beta_c^Tx+\gamma_c}}{\sum_{c\prime}e^{\beta_{c\prime}^Tx+\gamma_{c\prime}}}=S(\eta)_c \end{equation}

其中$\eta = [\beta_1^Tx+\gamma_1,...,\beta_C^Tx+\gamma_c]$,$S$为softmax函数(类似于max函数,故得此名),定义如下:

若将$\eta_c$除以一个常数(temperature),当$T\to 0$时，我们有:

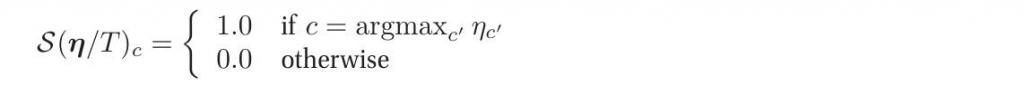
换句话说，当温度很低时，分布集中在概率最大的那个状态上，而当温度高时，所有的状态呈现均匀分布。

NOTE:该术语来自于统计物理学，在统计物理学中，人们更倾向于使用波尔兹曼分布（Boltzmann distribution）一词。

关于式16有一个有趣的性质，即对该式取log,我们则会得到一个关于$x$的线性方程。因此对于任意两类之间的决策边界将会是一条直线，据此该模型也被称为线性判别分析(Linear Discriminant Analysis,LDA)。而且对于二分类问题，我们可以得到:

\begin{equation} p(y=c|x,\theta) = p(y=c\prime|x,\theta) \end{equation}

\begin{equation} \beta_c^Tx+\gamma_c = \beta_{c\prime}^Tx+\gamma_{c\prime} \end{equation}

\begin{equation} x^T(\beta_{c\prime}-\beta_c) = \gamma_{c\prime}-\gamma_c \end{equation}

Two-class LDA

为了加深对以上等式的理解，对于二分类的情况，我们做如下说明:

\begin{equation} \begin{split} p(y=1|x,\theta) &= \frac{e^{\beta_1^Tx+\gamma_1}}{e^{\beta_1^Tx+\gamma_1}+e^{\beta_0^Tx+\gamma_0}} \\ &= \frac{1}{1+e^{(\beta_0-\beta_1)^Tx+(\gamma_0-\gamma_1)}} \\ &=sigm((\beta_1-\beta_0)^Tx+(\gamma_1-\gamma_0)) \end{split} \end{equation}

其中,$sigm(\eta)$代表Sigmoid函数。

现有:

\begin{equation} \begin{split} \gamma_1-\gamma_0 &= -{1 \over 2}\mu_1^T\Sigma^{-1}\mu_1+{1 \over 2}\mu_0^T\Sigma^{-1}\mu_0+log(\pi_1/\pi_0) \\ &=-{1 \over 2}(\mu_1-\mu_0)^T\Sigma^{-1}(\mu_1+\mu_0)+log(\pi_1/\pi_0) \end{split} \end{equation}

因此若我们另:

\begin{equation} \begin{split} \omega &= \beta_1-\beta_0 = \Sigma^{-1}(\mu_1-\mu_0) \\ x_0 &= {1 \over 2}(\mu_1+\mu_0)-(\mu_1-\mu_0)\frac{log(\pi_1/\pi_0)}{(\mu_1-\mu_0)^T\Sigma^{-1}(\mu_1-\mu_0)} \end{split} \end{equation}

则有$\omega^Tx_0 = -(\gamma_1-\gamma_0)$,即:

\begin{equation} p(y=1|x,\theta) = sigm(\omega^T(x-x_0)) \end{equation}

因此最后的决策规则很简单:将$x$平移$x_0$,然后投影到$\omega$上，通过结果是正还是负决定它到底属于哪一类。

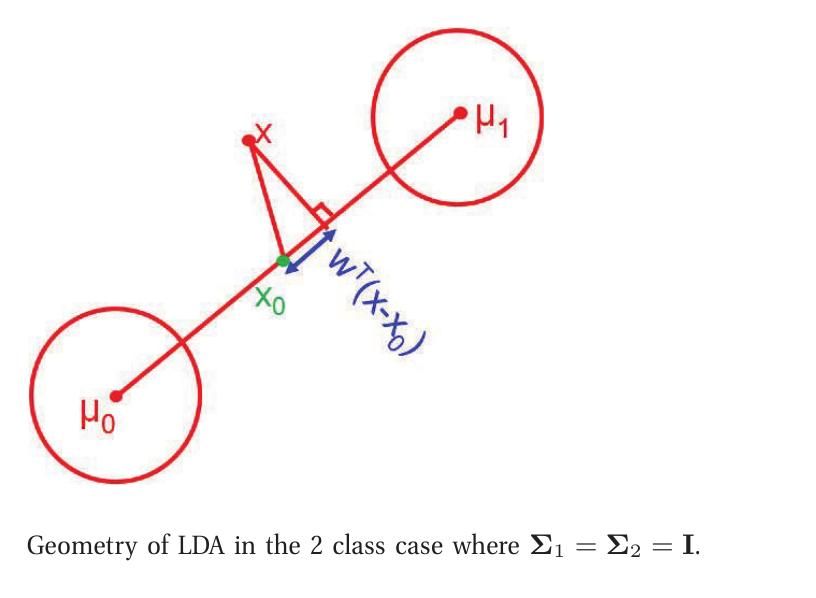
当$\Sigma = \sigma^2I$时，$\omega$与$\mu_1-\mu_0$同向。这时我们只需要判断投影点离$\mu_1$和$\mu_0$中的那个点近。当它们的先验概率$\pi_1 = \pi_0$时，投影点位于其中点；当$\pi_1>\pi_0$时，则$x_0$越趋近于$\mu_0$,直线的更大部分先验地属于类1;反之亦然。¹

Inference in joint Gaussian distributions

---

给定联合概率分布$p(x_1,x_2)$,如果我们能够计算边际概率分布$p(x1)$以及条件概率分布$p(x_1|x_2)$想必是极好的而且是及有用的。以下我们仅给出结论,下式表明如果两变量符合联合高斯分布，则它们的边际分布以及条件分布也都是高斯分布。

Theorem 3.2² 假定$x=(x_1,x_2)$服从联合高斯分布,且参数如下: \begin{equation} \mu = \left( \begin{array}{ccc} \mu_1 \\ \mu_2 \end{array} \right) \end{equation} \begin{equation} \Sigma = \left( \begin{array}{ccc} \Sigma_{11} & \Sigma_{12} \\ \Sigma_{21} & \Sigma_{22} \end{array} \right) \end{equation} 则我们可以得到如下边际概率分布: \begin{equation} p(x_1) = N(x_1|\mu_1,\Sigma_{11}) \\ p(x_2) = N(x_2|\mu_2,\Sigma_{22}) \end{equation} 另其后验条件分布为: \begin{equation} p(x_1|x_2) = N(x_1|\mu_{1|2},\Sigma_{1|2}) \end{equation} \begin{equation} \begin{split} \mu_{1|2} &= \mu_1+\Sigma_{12}\Sigma_{22}^{-1}(x_2-\mu_2) \\ &=\mu_1-\Lambda_{11}^{-1}\Lambda_{12}(x_2-\mu_2) \\ &=\Sigma_{1|2}(\Lambda_{11}\mu_1-\Lambda_{12}(x_2-\mu_2)) \\ \end{split} \end{equation} \begin{equation} \Sigma_{1|2} = \Sigma_{11}-\Sigma_{12}\Sigma_{22}^{-1}\Sigma_{21}=\Lambda_{11}^{-1} \end{equation}

Linear Gaussian Systems

---

给定两变量，$x$和$y$.令$x \in R^{D_x}$为一隐含变量,$y \in R^{D_y}$为关于$x$的包含噪声的观察值。此外，我们假定存在如下prior和likelihood: \begin{equation} \begin{split} p(x) &= N(x|\mu_x,\Sigma_x) \\ p(y|x) &= N(y|Ax+b,\Sigma_y) \end{split} \end{equation} 上式即称为Linear Gaussian System。此时我们有:

Theorem 3.3³ 给定一Linear Gaussian System.其后验分布$p(x|y)$具有如下形式: \begin{equation} \begin{split} p(x|y) &= N(x|\mu_{x|y},\Sigma_{x|y}) \\ \Sigma_{x|y}^{-1} &= \Sigma_x^{-1}+A^T\Sigma_y^{-1}A \\ \mu_{x|y} &= \Sigma_{x|y}[A^T\Sigma_y^{-1}(y-b)+\Sigma_x^{-1}\mu_x] \end{split} \end{equation}

Inferring an unknown vector from noisy measurements

下面我们举一个简单的例子以进一步说明Linear Gaussian System: 现有$N$个观测向量,$y_i \sim\ N(x,\Sigma_y)$,prior服从高斯分布$x \sim\ N(\mu_0,\Sigma_0)$.令$A=I,b=0$,此外，我们采用$\bar{y}$作为我们的有效估计值,其精度为$N\Sigma_y^{-1},$我们有: \begin{equation} \begin{split} p(x|y_1,...,y_N) &= N(x|\mu_N,\Sigma_N) \\ \Sigma_N^{-1} &= \Sigma_{0}^{-1}+N\Sigma_{y}^{-1} \\ \mu_N &= \Sigma_N(\Sigma_y^{-1}(N\bar{y})+\Sigma_0^{-1}\mu_0) \end{split} \end{equation} 为了更直观地解释以上模型,如下图所示:

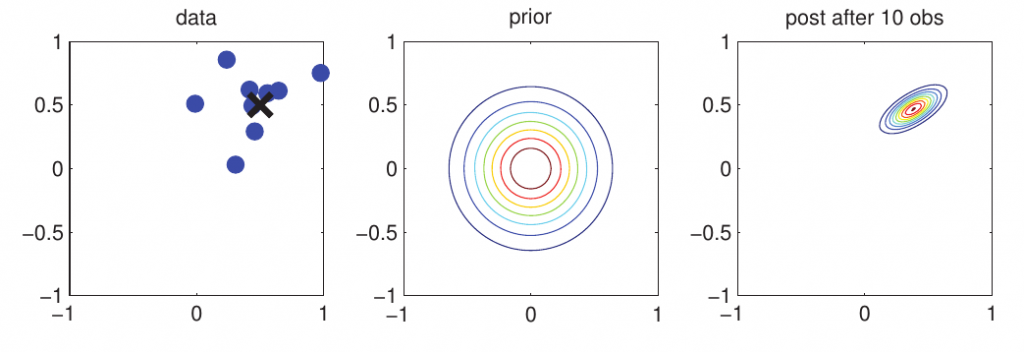
我们可将x视为2维空间中一个物体的真实位置(但我们并不知道),例如一枚导弹或者一架飞机,$y_i$则是我们的观测值(含噪声),可以视为雷达上的一些点。当我们得到越来越多的点时，我们就能够更好地进行定位。⁴

现假定我们有多个测量设备，且我们想利用多个设备的观测值进行估计，这种方法称为sensor fusion.如果我们有具有不同方差的多组观测值，那么posterior将会是它们的加权平均。如下图所示:

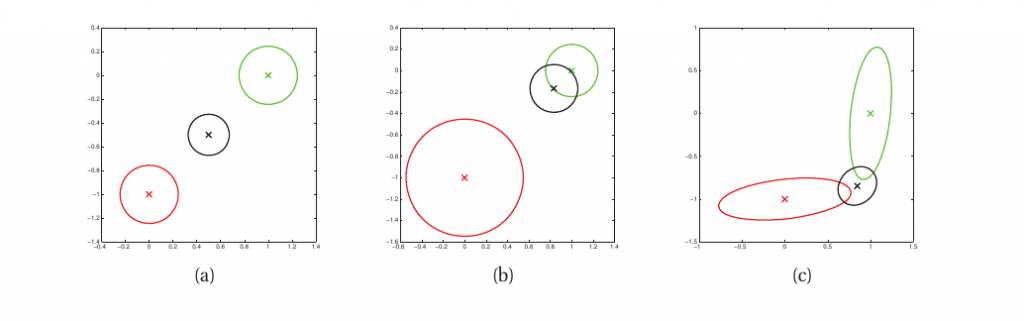
我们采用不带任何信息的关于$x$的先验分布，即$p(x)=N(\mu_0,\Sigma_0)=N(0,10^10I_2)$,我们得到2个观测值,$y_1 \sim\ N(x,\Sigma_{y,1}$,$y_2 \sim\ N(x,\Sigma_{y,2})$,我们需要计算$p(x|y_1,y_2)$.

如上图(a),我们设定$\Sigma_{y,1} = \Sigma_{y,2} = 0.01I_2$,因此两个传感器都相当可靠，posterior mean即位于两个观测值中间；如上图(b)，我们设定$\Sigma_{y,1}=0.05I_2$且$\Sigma_{y,2}=0.01I_2$,因此传感器2比传感器1可靠，此时posterior mean更靠近于$y_2$;如上图(c),我们有: \begin{equation} \Sigma_{y,1} = 0.01 \left( \begin{array}{cc} 10 & 1 \\ 1 & 1 \end{array} \right), \Sigma_{y,2} = 0.01 \left( \begin{array}{cc} 1 & 1 \\ 1 & 10 \end{array} \right) \end{equation}

从上式我们不难看出，传感器1在第2个分量上更可靠，传感器2在第1个分量上也更可靠。此时，posterior mean采用传感器1的第二分量以及传感器1的第二分量。

NOTE:当sensor测量精度未知时，我们则需要它们的测量精度也进行估计。

The Wishart Distribution

---

在多变量统计学中,Wishart分布是继高斯分布后最重要且最有用的模型。 ------Press

既然Press他老人家都说了Wishart分布很重要，而且我们下一部分会用到它，那么我们就必须得介绍介绍它了。(它主要被用来Model关于协方差矩阵的不确定性)

Wishart Distribution

Wishart概率密度函数具有如下形式: \begin{equation} Wi(\Lambda|S,\nu)=\frac{1}{Z_{Wi}}|\Lambda|^{(\nu-D-1)/2}exp(-{1 \over 2}tr(\Lambda S^{-1})) \end{equation}

其中,$\nu$为自由度，$S$为缩放矩阵。其归一项具有如下形式:(很恐怖，对吧!) \begin{equation} Z_{Wi}=2^{\nu D/2}\Gamma_D(\nu/2)|S|^{\nu/2} \end{equation}

其中,$\Gamma_D(a)$为多变量Gamma函数: \begin{equation} \Gamma_D(x) = \pi^{D(D-1)/4}\prod_{i=1}^{D} \Gamma(x+(1-i)/2) \end{equation}

于是有$\Gamma_1(a)=\Gamma(a)$且有: \begin{equation} \Gamma_D(\nu_0/2)=\prod_{i=1}^{D} \Gamma(\frac{\nu_0+1-i}{2}) \end{equation}

仅当$\nu>D-1$时归一项存在。

其实Wishart分布和Gaussian分布是有联系的。具体而言，令$x_i \sim\ N(0,\Sigma)$,则离散度矩阵$S=\sum_{i=1}^{N}x_ix_i^T$服从Wishart分布,且$S \sim\ Wi(\Sigma,1)$。于是有$E(S)=N\Sigma$.

更一般地，我们可以证明$Wi(S,\nu)$的mean和mode具有如下形式: \begin{equation} mean=\nu S,mode=(\nu-D-1)S \end{equation}

仅当$\nu>D+1$时mode存在。

当$D=1$时，Wishart分布退化为Gamma分布，且有: \begin{equation} Wi(\lambda|s^{-1},v) = Ga(\lambda|{\nu \over 2},{s \over 2}) \end{equation}

Inverse Wishart Distribution

若$\Sigma^{-1} \sim\ Wi(S,\nu)$,则$\Sigma \sim\ IW(S^{-1},\nu+D+1)$,其中$IW$为逆Wishart分布。当$\nu>D-1$且$S \succ 0$时,我们有: \begin{equation} \begin{split} IW(\Sigma|S,\nu) &= \frac{1}{Z_{IW}}|\Sigma|^{-(\nu+D+1)/2}exp(-{1 \over 2}tr(S^{-1}\Sigma^{-1})) \\ Z_{IW} &= |S|^{-\nu/2}2^{\nu D/2}\Gamma_D(\nu/2) \end{split} \end{equation}

此外我们可以证明逆Wishart分布具有如下性质: \begin{equation} mean=\frac{S^{-1}}{\nu-D-1},mode=\frac{S^{-1}}{\nu+D+1} \end{equation}

当$D=1$时,它们退化为逆Gamma分布: \begin{equation} IW(\sigma^2|S^{-1},\nu)=IG(\sigma^2|\nu/2,S/2) \end{equation}

Inferring the parameters of an MVN⁵

---

到目前为止，我们已经讨论了在$\theta=(\mu,\Sigma)$已知的条件下如何inference，现我们讨论一下如何对参数本身进行估计。假定$x_i \sim\ N(\mu,\Sigma)$ for $i=1:N$.本节主要分为两个部分:

• 计算$p(\mu|D,\Sigma)$;
• 计算$p(\Sigma|D,\mu)$.

Posterior distribution of $\mu$

我们已经就如何计算$\mu$的极大似然估计值进行了讨论,现我们讨论如何计算其posterior.

其likelihood具有如下形式: \begin{equation} p(D|\mu) = N(\bar{x}|\mu,{1 \over N}\Sigma) \end{equation}

为了简便起见，我们采用共轭先验分布，即高斯。特别地，若$p(\mu)=N(\mu|m_0,V_0)$.此时我们可以根据之前Linear Gaussian System的结论得到(和我们之前提到的雷达的例子雷同): \begin{equation} \begin{split} p(\mu|D,\Sigma) &= N(\mu|m_N,V_N) \\ V_N^{-1} &= V_0^{-1}+N\Sigma^{-1} \\ m_N &= V_N(\Sigma^{-1}(N\bar{x})+V_0^{-1}m_0) \end{split} \end{equation}

我们可以通过设定$V_0 = \infty I$提供一个不带任何信息的先验，此时我们有$p(\mu|D,\Sigma)=N(\bar{x},{1 \over N}\Sigma)$,即和MLE得到的结果相同。

Posterior distribution of $\Sigma$

现我们讨论如何计算$p(\Sigma|D,\mu)$,其likelihood具有如下形式:⁶ \begin{equation} p(D|\mu,\Sigma) \propto |\Sigma|^{-{N \over 2}}exp(-{1 \over 2}tr(S_{\mu}\Sigma^{-1})) \end{equation}

之前我们提到过如果采用共轭先验能够减少计算的复杂度，而此likelihood的共轭先验就是我们之前提到的非常恐怖的逆Wishart分布，即:

\begin{equation} IW(\Sigma|S_0^{-1},\nu_0) \propto |\Sigma|^{-(\nu_0+D+1)/2}exp(-{1 \over 2}tr(S_0\Sigma^{-1})) \end{equation}

上式中$N_0=\nu+D+1$控制着先验的强度,和likelihood中的$N$的作用基本相同。

将先验和likelihood相乘我们得到如下posterior:

\begin{equation} \begin{split} p(\Sigma|D,\mu) &\propto |\Sigma|^{-{N \over 2}}exp(-{1 \over 2}tr(S_{\mu}\Sigma^{-1}))|\Sigma|^{-(\nu_0+D+1)/2}exp(-{1 \over 2}tr(S_0\Sigma^{-1})) \\ &=|\Sigma|^{-\frac{N+(\nu_0+D+1)}{2}}exp(-{1 \over 2}tr(\Sigma^{-1}(S_{\mu}+S_0))) \\ &=IW(\Sigma|S_N,\nu_N) \\ \nu_N &= \nu_0+N \\ S_N^{-1} &= S_0+S_{\mu} \end{split} \end{equation}

总而言之，从上式我们可以看到，posterior $v_N$的强度为$\nu_0$加$N$;posterior离散度矩阵是先验离散度矩阵$S_0$和数据离散度矩阵$S_{\mu}$之和。

MAP Estimation

根据我们之前得到的关于$\Sigma$的极大似然估计值,即:

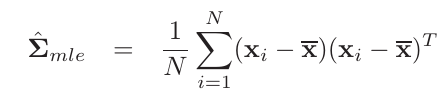
从上式我们可以看出矩阵的rank为$min(N,D)$。若$N$小于$D$,该矩阵不是full rank的，因此不可逆。另尽管$N$可能大于$D$,$\hat{\Sigma}$也可能是ill-conditioned(接近奇异)。

为了解决上述问题，我们可以采用posterior mean或mode.我们可以证明$\Sigma$的MAP估计值如下:(使用我们推导MLE时所用的技巧，其实并不难，亲证下式正确):

\begin{equation} \hat\Sigma_{MAP} = \frac{S_N}{\nu_N+D+1} = \frac{S_0+S_{\mu}}{N_0+N_{\mu}} \end{equation}

当我们采用improper uniform prior，即$S_0=0,N_0=0$时，我们即得MLE估计值。

当$D/N$较大时，选择一个包含信息的合适的prior就相当必要了。令$\mu=\bar{x}$,故有$S_{\mu}=S_{\bar{x}}$,此时MAP估计值可被重写为prior mode和MLE的convex combination.令$\Sigma_0 \triangleq \frac{S_0}{N_0}$为prior mode,则有:

\begin{equation} \begin{split} \hat\Sigma_{MAP} = \frac{S_0+S_{\bar{x}}}{N_0+N} &= \frac{N_0}{N_0+N}\frac{S_0}{N_0}+\frac{N}{N_0+N}\frac{S}{N} \\ &=\lambda\Sigma_0+(1-\lambda)\hat{\Sigma}_{mle} \end{split} \end{equation}

其中$\lambda=\frac{N_0}{N_0+N}$,控制着向prior shrinkage的程度。对于$\lambda$而言，我们可以通过交叉验证设置其值。⁷

而对于先验的协方差矩阵$S_0$,一般采用如下prior:$S_0=diag(\hat{\Sigma}_{mle})$.因此，我们有:

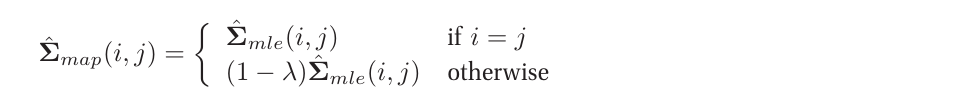
由上式我们可以看出，对角线的元素和极大似然估计值相等，而非对角线则趋近于0.因此该技巧也被称为shrinkage estimation,or regularized estimation.

1. LDA算法可能导致overfitting,具体解决方法请参阅Machine Learning:a probabilistic perspective一书4.2.*部分 ↩
2. 具体证明请参考ML:APP一书4.3.4.3一节 ↩
3. 证明请参考ML:APP一书4.4.3节 ↩
4. 另外一种方法为Kalman Filter Algorithm ↩
5. 本部分部分参考Regularized Gaussian Covariance Estimation ↩
6. 参见MLE for Gaussian部分 ↩
7. 其他方法见ML:APP一书4.6.2.1节 ↩

---