本文主要对之前看过的Machine Learning:A Probabilistic Perspective一书中有关离散数据生成模型、高斯模型以及线性模型的相关部分进行梳理。

Closed Form¹

在阅读Machine Learning:A Probabilistic Perspective这本书的时候经常看到Closed Form这个词。以下给出一简单说明:

如果一个表达式可以表示成有限的某些特定的Ｗell-known函数的形式，那么我们说这个表达式是一个Closed Form表达式。一般而言,这些Well-known函数包括基本的函数，如常数、单个变量$x$、基本的算术操作、开方、指数对数函数、三角反三角函数等。如果一个问题可以得到一Closed Form的解,我们通常就说这个问题是可解的。

Closed–form表达式是解析表达式的一个非常重要的子类,解析表达式可包含有限或无限个Well-known函数。和更为广泛的解析表达式不同,Closed–form表达式并不包含无限级数和递归分数(Continued Fractions)形式，也不能包含积分和极限。

一个方程或方程组当且仅当它的一个解可写成Closed-Form形式时,我们才说该方程或方程组具有一Closed-form solution.类似地,一个方程或方程组当且仅当它的一个解可写成解析形式时,我们才说该方程或方程组具有一解析解。

Gaussian Models²

Diagonal LDA

在GLA中,如果我们限定不同类间共享$\Sigma$,并对每类使用一对角协方差矩阵，我们得到的模型则称为Diagonal LDA Model.对应的判别函数如下所示:

\begin{equation} \delta_c(x) = log\ p(x,y=c|\theta) = -\sum_{j=1}^D \frac{(x_j-\mu_{cj})^2}{2\sigma_j^2}+log\ \pi_c \end{equation}

一般我们令$\hat\mu_{cj} = \bar{x}_{cj}$且$\hat\sigma_j^2=s_j^2$,$s_j^2$称为Pooled empirical variance,定义如下:

\begin{equation} s_j^2 = \frac{\sum_{c=1}^C \sum_{i:y_i=c} (x_{ij} - \bar{x}_{cj})^2}{N-C} \end{equation}

在高维情形下,该模型比LDA和RDA效果都要好。

方差MAP估计

ML(指Machine Learning:A Probabilistic Perspective,以后如果不作说明,也指该书)一书中关于$\Sigma$的估计写的很复杂,于是基本上没看那部分,关于$\Sigma$的MAP估计可参考以下链接:

Regularized Gaussian Covariance Estimation

Linear Regression³

Bayesian Linear Regression

给定训练集$D={(x_i,y_i)|i=1,\cdots,n}$,我们有:

对于Linear Regression,我们有:

\begin{equation} \begin{split} f(x) & = x^Tw \in R,x,w \in R^D \\ y &= f(x) + \epsilon = x^Tw+\epsilon \in R \\ \epsilon &\sim\ N(0,\sigma^2) \in R \end{split} \end{equation}

我们首先计算Likelihood:

\begin{equation} \begin{split} P(y|X,w) &= \prod_{i=1}^n P(y_i|x_i^Tw) \\ &= \prod_{i=1}^n N_{yi}(x_i^Tw,\sigma^2) \\ &= \prod_{i=1}^n \frac{1}{\sqrt{2\pi\sigma^2}}exp[\frac{-(y_i-x_i^Tw)^2}{2\sigma^2}] \\ &= \frac{1}{(2\pi\sigma^2)^{n/2}}exp[\frac{-1}{2\sigma^2}||y-X^Tw||^2] \\ &= N_y(X^Tw,\sigma^2I_n) \end{split} \end{equation}

另我们假定Prior服从$w \sim\ N_w(0,\Sigma_p)$

则我们可得Posterior:

\begin{equation} \begin{split} P(w|X,y) &= \frac{P(y|X,w)P(w)}{P(y|X)} \\ &= \frac{P(y|X,w)P(w)}{\int P(y|X,w)dw} \\ &= \frac{N_y(X^Tw,\sigma^2I_n)N_w(0,\Sigma_p)}{\int N_y(X^Tw,\sigma^2I_n)N_w(0,\Sigma_p)dw} \\ &\sim\ N_y(X^Tw,\sigma^2I_n)N_w(0,\Sigma_p) \end{split} \end{equation}

更进一步地,我们有:

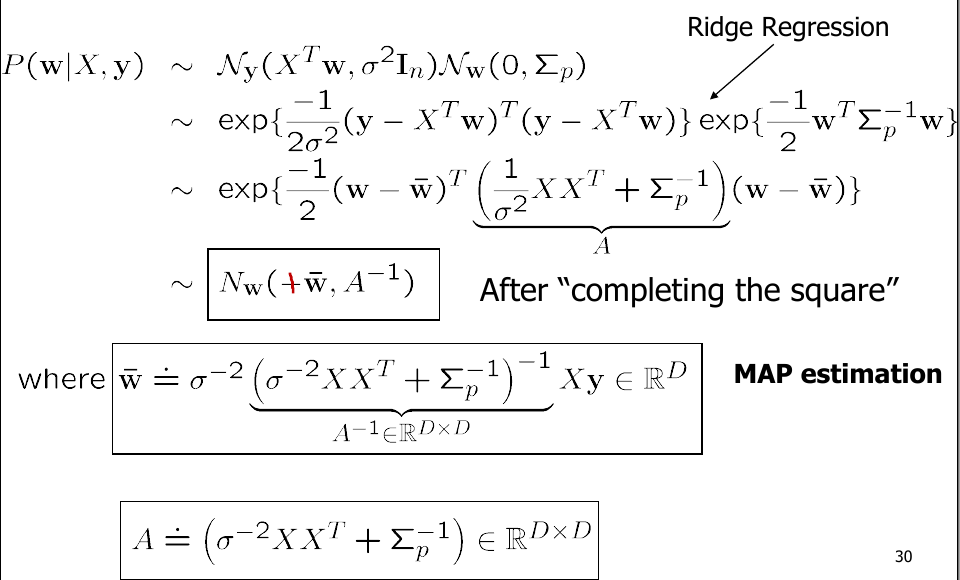
NOTE:Posterior协方差矩阵并不依赖观察值$y$.

我们希望使用以上得到的Posterior计算$f$在点$x_{*}$处的值,我们有:

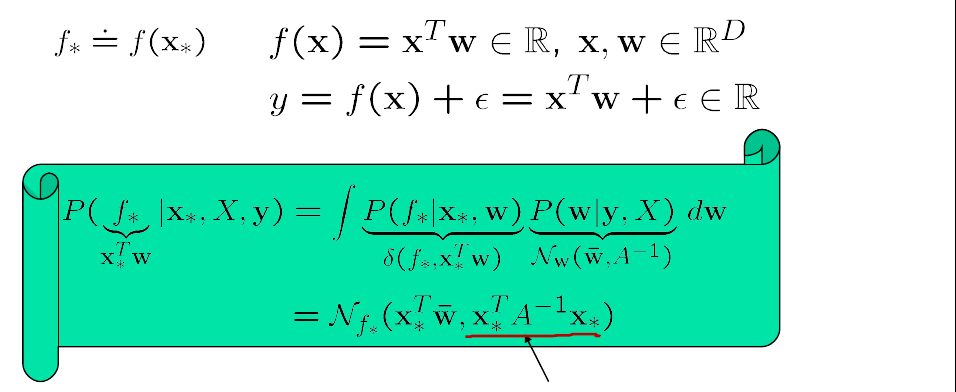
Logistic Regression⁴

ML一书中给出的形式并不便于计算Gradient以及Hessian,以下根据李航统计学习方法中的相关内容给出以下较易计算的形式。

对于给定的训练集$T={(x_1,y_1),(x_2,y_2),\cdots,(x_N,y_N)}$,其中,$x_i \in R^n,y_i \in {0,1}$,我们令:

\begin{equation} P(Y=1|x) = \mu(x),P(Y=0|x) = 1-\mu(x) \end{equation}

对数似然函数为: \begin{equation} \begin{split} \ell(w) &= \sum_{i=1}^N [y_i log \mu(x_i)+(1-y_i)log(1-\mu(x_i))] \\ &= \sum_{i=1}^N [y_i log \frac{\mu(x_i)}{1-\mu(x_i)}+log(1-\mu(x_i))] \\ &= \sum_{i=1}^N [y_i(w^Tx_i)-log(1+exp(w^Tx_i)] \end{split} \end{equation}

为了使用最小值,在ML一书中用到的是Negetive Log Likelihood(NLL),特此说明。

由此我们得到:

\begin{equation} \begin{split} g &= \frac{df(w)}{dw} = \sum_i (\mu_i-y_i)x_i = X^T(\mu-y) \\ H &= \frac{dg(w)^T}{dw} = \sum_i (\bigtriangledown_w \mu_i)x_i^T \\ &= \sum_i \mu_i(1-\mu_i)x_ix_i^T \\ &= X^TSX \end{split} \end{equation}

其中,$S \triangleq diag(\mu_i(1-\mu_i))$.得到梯度和Hessian矩阵之后,以下我们就能使用最速下降、牛顿法、BFGS等方法对Logistic Regression进行求解了。

EM

本部分与ML一书第十一章无关,只是为了更清楚地了解EM算法。以下给出一个挺不错的PPT:

Tutorial EM

TODO Board

• Posterior Predicative for Multinomial-Dirichlet Models⁵
• Regularized LDA
• Nearest shrunken centroids classifier
• Numerically stable computation[7.5.2]
• Connection with PCA[7.5.3]
• Estimating $\sigma^2$[7.6.3]
• Evidence Procedure[7.6.4]
• Conjugate Gradient(CG)
• BFGS(LBFGS)
• Multi-class Logistic Regression and Maximum Entropy Classfier
• Bayesian Logistic Regression[8.4]
• Online Learning[8.5]
• Generative vs Discriminative Classfiers[8.6]

1. Closed-form expression ↩
2. Machine Learning:A Probabilistic Perspective Chapter 4 ↩
3. Machine Learning:A Probabilistic Perspective Chapter 7 ↩
4. Machine Learning:A Probabilistic Perspective Chapter 8 ↩
5. Machine Learning:A Probabilistic Perspective Chapter 3 ↩