因子分析

---

问题

当样本个数$m$远远大于其特征个数$n$时，这样不管是进行回归、聚类等都没有太大的问题。然而当训练样例个数$m$太小，甚至$m \ll n$的时候，使用梯度下降法进行回归时，如果初值不同，得到的参数结果会有很大偏差（因为方程数小于参数个数）。另外，如果使用多元高斯分布(Multivariate Gaussian distribution)对数据进行拟合时，也会有问题。让我们来演算一下，看看会有什么问题：

多元高斯分布的参数估计公式如下:

\begin{equation} \begin{split} \mu &= {1 \over m}\sum_{i=1}^m x^{(i)} \\ \Sigma &= {1 \over m}\sum_{i=1}^m (x^{(i)}-\mu)(x^{(i)}-\mu)^T \end{split} \end{equation}

其中,$x^{(i)}$表示样例，共有$m$个，每个样例$n$个特征，因此$\mu$是$n$维向量，$\Sigma$是$n*n$协方差矩阵。

当$m \ll n$时，我们会发现$\Sigma$是奇异阵($|\Sigma|=0$)，也就是说$\Sigma^{-1}$不存在，没办法拟合出多元高斯分布了，确切的说是我们估计不出来$\Sigma$。

如果我们仍然想用多元高斯分布来估计样本，那怎么办呢？

限制协方差矩阵

当没有足够的数据去估计$\Sigma$时，那么只能对模型参数进行一定假设，之前我们想估计出完全的$\Sigma$(矩阵中的全部元素），现在我们假设$\Sigma$就是对角阵（各特征间相互独立），那么我们只需要计算每个特征的方差即可，最后的$\Sigma$只有对角线上的元素不为0.

\begin{equation} \Sigma_{jj} = {1 \over m}\sum_{i=1}^m (x_j^{(i)}-\mu_j)^2 \end{equation}

回想我们之前在Gaussian Models一文中讨论过的二维多元高斯分布的几何特性，在平面上的投影是个椭圆，中心点由$\mu$决定，椭圆的形状由$\Sigma$决定。$\Sigma$如果变成对角阵，就意味着椭圆的两个轴都和坐标轴平行了。

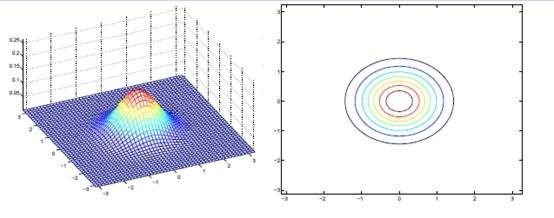
如果我们想对$\Sigma$进一步限制的话，可以假设对角线上的元素都是等值的。

\begin{equation} \Sigma = \sigma^2 I \end{equation}

其中:

\begin{equation} \sigma^2 = \frac{1}{mn}\sum_{j=1}^n \sum_{i=1}^m (x_j^{(i)}-\mu_j)^2 \end{equation}

也就是上一步对角线上元素的均值，反映到二维高斯分布图上就是椭圆变成圆。

当我们要估计出完整的$\Sigma$时，我们需要$m>=n+1$才能保证在最大似然估计下得出的$\Sigma$是非奇异的。然而在上面的任何一种假设限定条件下，只要$m>=2$都可以估计出限定的$\Sigma$。

这样做的缺点也是显然易见的，我们认为特征间独立，这个假设太强。接下来，我们给出一种称为因子分析的方法，使用更多的参数来分析特征间的关系，并且不需要计算一个完整的$\Sigma$。

因子分析

下面通过一个简单例子，来引出因子分析背后的思想。

因子分析的实质是认为$m$个$n$维特征的训练样例$x^{(i)}$的产生过程如下：

• 首先在一个$k$维的空间中按照多元高斯分布生成$m$个$z^{(i)}$（$k$维向量),即

\begin{equation} z^{(i)} \sim\ N(0,I) \end{equation}

• 然后存在一个变换矩阵$\Lambda \in R^{n*k}$，将$z^{(i)}$映射到$n$维空间中，即

\begin{equation} \Lambda z^{(i)} \end{equation}

因为$z^{(i)}$的均值是0，映射后仍然是0。

• 然后将$\Lambda z^{(i)}$加上一个均值$\mu$（$n$维），即

\begin{equation} \mu + \Lambda z^{(i)} \end{equation}

对应的意义是将变换后的$\Lambda z^{(i)}$（$n$维向量）移动到样本$x^{(i)}$的中心点$\mu$。

• 由于真实样例$x^{(i)}$与上述模型生成的有误差，因此我们继续加上误差$\epsilon$($n$维向量),而且$\epsilon$符合多元高斯分布，即

\begin{equation} \begin{split} \epsilon \sim\ N(0,\mathbf \Psi) \\ \mu + \Lambda z^{(i)} + \epsilon \end{split} \end{equation}

• 最后的结果认为是真实的训练样例$x^{(i)}$的生成公式

\begin{equation} x^{(i)} = \mu + \Lambda z^{(i)} + \epsilon \end{equation}

让我们使用一种直观方法来解释上述过程：

假设我们有$m=5$个2维的样本点$x^{(i)}$（两个特征），如下：

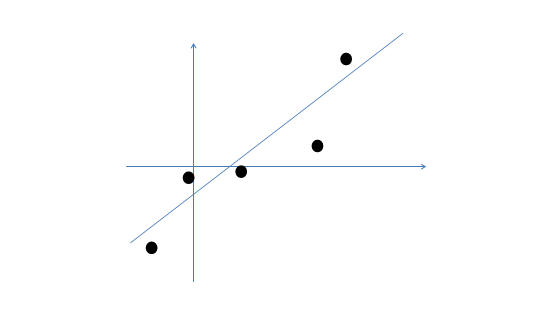
那么按照因子分析的理解，样本点的生成过程如下：

• 我们首先认为在1维空间（这里$k=1$），存在着按正态分布生成的$m$个点$z^{(i)}$，如下:

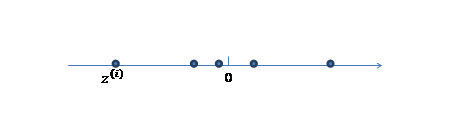
均值为0，方差为1。

• 然后使用某个$\Lambda=(a,b)^T$将一维的$z$映射到2维，图形表示如下：

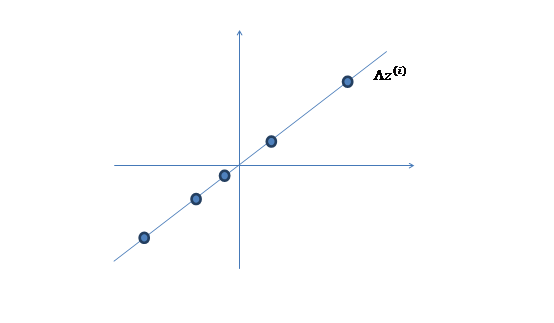
• 之后加上$\mu\ (\mu_1,\mu_2)^T$，即将所有点的横坐标移动$\mu_1$，纵坐标移动$\mu_2$，将直线移到一个位置，使得直线过点$\mu$，原始左边轴的原点现在为$\mu$(红色点)。

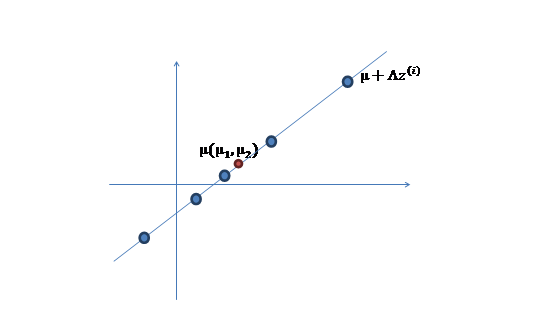
然而，样本点不可能这么规则，在模型上会有一定偏差，因此我们需要将上步生成的点做一些扰动（误差），扰动$\epsilon \sim\ N(0,\mathbf \Psi)$。

• 加入扰动后，我们得到黑色样本$x^{(i)}$如下：

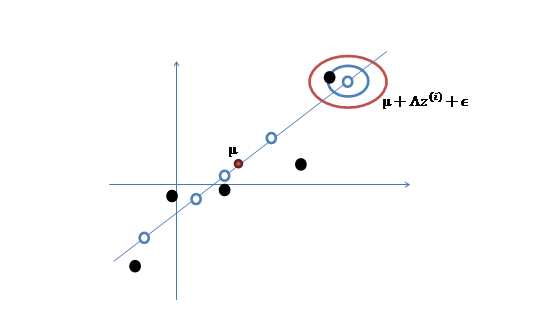
• 其中由于$z$和$\epsilon$的均值都为0，因此$\mu$也是原始样本点（黑色点）的均值。

由以上的直观分析，我们知道了因子分析其实就是认为高维样本点实际上是由低维样本点经过高斯分布、线性变换、误差扰动生成的，因此高维数据可以使用低维来表示。

因子分析模型

上面的过程是从隐含随机变量$z$经过变换和误差扰动来得到观测到的样本点。其中$z$被称为因子，是低维的。

我们将式子再列一遍如下：

\begin{equation} \begin{split} z &\sim\ N(0,I) \\ \epsilon &\sim\ N(0,\mathbf \Psi) \\ x &= \mu + \Lambda z + \epsilon \end{split} \end{equation}

其中误差$\epsilon$和$z$是独立的。

下面使用的因子分析表示方法是矩阵表示法，在参考资料中给出了一些其他的表示方法，如果不明白矩阵表示法，可以参考其他资料。

矩阵表示法认为$z$和$x$联合符合多元高斯分布，如下:

\begin{equation} \left[ \begin{array}{cc} z \\ x \end{array} \right]\sim\ N(\mu_{zx},\Sigma) \end{equation}

求$\mu_{zx}$之前需要求$E[x]$

\begin{equation} \begin{split} E[x] &= E[\mu + \Lambda z + \epsilon] \\ &= \mu + \Lambda E[z] + E[\epsilon] \\ &= \mu \end{split} \end{equation}

我们已知$E[z]=0$，因此:

\begin{equation} \mu_{zx} = \left[ \begin{array}{cc} 0 \\ \mu \end{array} \right] \end{equation}

下一步是计算$\Sigma$，其中$\Sigma_{zz} = Cov(z) = I$.接着求$\Sigma_{zx}$

\begin{equation} \begin{split} E[(z-E[z])(x-E[x])^T] &= E[z(\mu + \Lambda z + \epsilon - \mu)^T] \\ &= E[zz^T]\Lambda^T + E[z\epsilon^T] \\ &= \Lambda^T \end{split} \end{equation}

这个过程中利用了$z$和$\epsilon$独立假设($E[z\epsilon^T] = E[z]E[\epsilon^T]=0$)。并将$\Lambda$看作已知变量。

接着求$\Sigma_{xx}$

\begin{equation} \begin{split} E[(x-E(x))(x-E[x])^T] &= E[(\mu+\Lambda z+\epsilon -\mu)(\mu+\Lambda z+\epsilon -\mu)^T] \\ &= E[\Lambda zz^T \Lambda^T+ \epsilon z^T \Lambda^T+\Lambda z \epsilon^T+\epsilon \epsilon^T] \\ &= \Lambda E[zz^T] \Lambda^T + E[\epsilon \epsilon^T] \\ &= \Lambda \Lambda^T + \mathbf \Psi \end{split} \end{equation}

然后得出联合分布的最终形式:

\begin{equation} \left[ \begin{array}{cc} z \\ x \end{array} \right] \sim\ N\left( \left[ \begin{array}{cc} 0 \\ \mu \end{array} \right], \left[ \begin{array}{cc} I & \Lambda^T \\ \Lambda & \Lambda \Lambda^T + \mathbf \Psi \end{array} \right] \right) \end{equation}

从上式中可以看出$x$的边缘分布为$x \sim\ N(\mu,\Lambda \Lambda^T + \mathbf \Psi)$.

那么对样本${x^{(i);i=1,...,m}}$进行最大似然估计

\begin{equation} \ell(\mu,\Lambda,\mathbf \Psi) = log \prod_{i=1}^m \frac{1}{(2\pi)^{n/2} |\Lambda \Lambda^T+\mathbf \Psi|}exp(-{1 \over 2}(x^{(i)}-\mu)^T(\Lambda \Lambda^T + \mathbf \Psi)^{-1} (x^{(i)}-\mu)) \end{equation}

然后对各个参数求偏导数不就得到各个参数的值了么？可惜我们得不到closed-form。想想也是，如果能得到，还干嘛将$z$和$x$放在一起求联合分布呢。根据之前对参数估计的理解，在有隐含变量$z$时，我们可以考虑使用EM来进行估计。

因子分析的EM估计

我们先来明确一下各个参数,$z$为隐含变量,$\mu,\Lambda,\mathbf \Psi$为待估参数。

回想EM算法两个步骤:

循环重复直至收敛{

(E Step)对于每一个$i$,计算: \begin{equation} Q_i(z^{(i)}) := p(z^{(i)}|x^{(i)};\theta) \end{equation} (M Step)计算: \begin{equation} \theta := arg max_{\theta} \sum_{i} \sum_{z^{(i)}} Q_i(z^{(i)}) \ log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} \end{equation} }

我们套用一下:

(E Step):

\begin{equation} Q_i(z^{(i)}) := p(z^{(i)}|\mu,\Lambda,\mathbf \Psi) \end{equation}

根据之前在Gaussian Models中提到过的Posterior Conditional的相关知识,我们有:

\begin{equation} \begin{split} \mu_{z^{(i)}|x^{i}} &= \Lambda^T (\Lambda \Lambda^T+\mathbf \Psi)^{-1}(x^{(i)}-\mu) \\ \Sigma_{z^{(i)}|x^{i}} &= I - \Lambda^T (\Lambda \Lambda^T+\mathbf \Psi)^{-1} \Lambda \end{split} \end{equation}

那么根据多元高斯分布公式，得到:

\begin{equation} Q_i(z^{(i)}) = \frac{1}{(2\pi)^{k/2}|\Sigma_{z^{(i)}|x^{(i)}}|^{1/2}}exp(-{1 \over 2}(z^{(i)}-\mu_{z^{(i)}|x^{(i)}})^T \Sigma_{z^{(i)}|x^{(i)}}^{-1} (z^{(i)}-\mu_{z^{(i)}|x^{(i)}})) \end{equation}

(M Step):

直接写要最大化的目标是:

\begin{equation} \sum_{i=1}^m \int_{z^{(i)}} Q_i(z^{(i)}) \ log \frac{p(x^{(i)},z^{(i)};\theta)}{Q_i(z^{(i)})} dz^{(i)} \end{equation}

其中待估参数是$\mu,\Lambda,\mathbf \Psi$.下面我们重点求$\Lambda$的估计公式

首先将上式简化为：

\begin{equation} \begin{split} \sum_{i=1}^m &\int_{z^{(i)}} Q_i(z^{(i)}) \ [log p(x^{(i)}|z^{(i)};\mu,\Lambda,\mathbf \Psi) +p(z^{(i)})-log\ Q_i(z^{(i)})]dz^{(i)} \\ &= \sum_{i=1}^m E_{z^{(i)} \sim\ Q_i} [log p(x^{(i)}|z^{(i)};\mu,\Lambda,\mathbf \Psi) +p(z^{(i)})-log\ Q_i(z^{(i)})] \end{split} \end{equation}

这里$z^{(i)} \sim\ Q_i$表示$z^{(i)}$服从$Q_i$分布。然后去掉与$\Lambda$不相关的项（后两项），得

\begin{equation} \begin{split} \sum_{i=1}^m & E[log p(x^{(i)}|z^{(I)};\mu,\Lambda,\Psi)] \\ &= \sum_{i=1}^m E[log \frac{1}{(2\pi)^{n/2}|\mathbf \Psi|^{1/2}}exp(-{1 \over 2}(x^{(i)}-\mu-\Lambda z^{(i)})^T |\mathbf \Psi|^{-1} (x^{(i)}-\mu-\Lambda z^{(i)})] \end{split} \end{equation}

去掉不相关的前两项后，对$\Lambda$求偏导得:

\begin{equation} \begin{split} \bigtriangledown_{\Lambda} & \sum_{i=1}^N -E[{1 \over 2}(x^{(i)}-\mu-\Lambda z^{(i)})^T |\mathbf \Psi|^{-1} (x^{(i)}-\mu-\Lambda z^{(i)})] \\ &= \sum_{i=1}^m \bigtriangledown_{\Lambda} E[- tr({1 \over 2}{z^{(i)}}^T\Lambda^T \Psi^{-1} z^{(i)}) + tr({z^{(i)}}^T\Lambda^T \Psi^{-1} (x^{(i)}-\mu))] \\ &= \sum_{i=1}^m \bigtriangledown_{\Lambda} E[- tr({1 \over 2}\Lambda^T \Psi^{-1} z^{(i)}{z^{(i)}}^T) + tr(\Lambda^T \Psi^{-1} (x^{(i)}-\mu){z^{(i)}}^T)] \\ &= \sum_{i=1}^m E[-\Psi^{-1} z^{(i)}{z^{(i)}}^T) + \Psi^{-1} (x^{(i)}-\mu){z^{(i)}}^T] \end{split} \end{equation}

最后让其值为0，并且化简得:

\begin{equation} \Lambda = (\sum_{i=1}^m (x^{(i)}-\mu) E_{z^{(i)} \sim\ Q_i}{z^{(i)}}^T)(\sum_{i=1}^m E_{z^{(i)} \sim\ Q_i}[{z^{(i)}z^{(i)}}^T])^{-1} \end{equation}

到这里我们发现，这个公式有点眼熟，与之前回归中的最小二乘法矩阵形式类似:

\begin{equation} \theta^T = (y^TX)(X^TX)^{-1} \end{equation}

这里解释一下两者的相似性，我们这里的$x$是$z$的线性函数（包含了一定的噪声）。在E步得到$z$的估计后，我们找寻的$\Lambda$实际上是$x$和$z$的线性关系。而最小二乘法也是去找特征和结果直接的线性关系。

到这还没完，我们需要求得括号里面的值.

根据我们之前对$z|x$的定义，我们知道:

\begin{equation} \begin{split} E_{z^{(i)} \sim\ Q_i}{z^{(i)}}^T &= \mu_{z^{(i)}|x^{(i)}}^T \\ E_{z^{(i)} \sim\ Q_i}[{z^{(i)}z^{(i)}}^T] &= \mu_{z^{(i)}|x^{(i)}} \mu_{z^{(i)}|x^{(i)}}^T + \Sigma_{z^{(i)}|x^{(i)}} \end{split} \end{equation}

将上式带入即可得到$\Lambda$的EM估计值。其他参数也可以通过类似的方法获得。

总结

根据上面的EM的过程，要对样本$X$进行因子分析，只需知道要分解的因子数($z$的维度)即可。通过EM，我们能够得到转换矩阵$\Lambda$和误差协方差$\Psi$。

因子分析实际上是降维，在得到各个参数后，可以求得$z$。但是$z$的各个参数含义需要自己去琢磨。

因子分析(Factor Analysis)是一种数据简化的技术。它通过研究众多变量之间的内部依赖关系，探求观测数据中的基本结构，并用少数几个假想变量来表示其基本的数据结构。这几个假想变量能够反映原来众多变量的主要信息。原始的变量是可观测的显在变量，而假想变量是不可观测的潜在变量，称为因子。

PCA

---

PCA的思想是将$n$维特征映射到$k$维上($k<n$），这$k$维是全新的正交特征。这$k$维特征称为主元，是重新构造出来的$k$维特征，而不是简单地从$n$维特征中去除其余$n-k$维特征。

PCA计算过程

首先介绍PCA的计算过程,假设我们得到的2维数据如下:

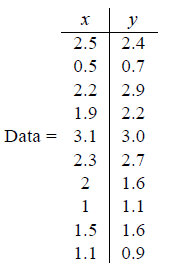
行代表了样例，列代表特征，这里有10个样例，每个样例两个特征。可以这样认为，有10篇文档，$x$是10篇文档中“learn”出现的TF-IDF，$y$是10篇文档中“study”出现的TF-IDF。也可以认为有10辆汽车，$x$是千米/小时的速度，$y$是英里/小时的速度，等等。

第一步:分别求$x$和$y$的平均值，然后对于所有的样例，都减去对应的均值。这里$x$的均值是1.81，$y$的均值是1.91，那么第一个样例减去均值后即为（0.69,0.49），得到

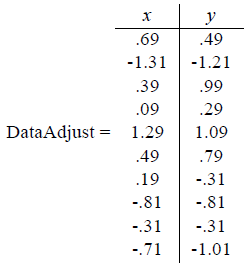
第二步，求特征协方差矩阵，如果数据是3维，那么协方差矩阵是

\begin{equation} C=\left( \begin{array}{cc} cov(x,x) & cov(x,y) & cov(x,z) \\ cov(y,x) & cov(y,y) & cov(y,z) \\ cov(z,x) & cov(z,y) & cov(z,z) \end{array} \right) \end{equation}

这里只有$x$和$y$，求解得

\begin{equation} cov=\left( \begin{array}{cc} .616555566 & .615444444 \\ .615444444 & .716555556 \end{array} \right) \end{equation}

对角线上分别是$x$和$y$的方差，非对角线上是协方差。协方差大于0表示$x$和$y$若有一个增，另一个也增；小于0表示一个增，一个减；协方差为0时，两者独立。协方差绝对值越大，两者对彼此的影响越大，反之越小。

第三步，求协方差的特征值和特征向量，得到:

\begin{equation} eigenvalues=\left( \begin{array}{cc} .0490833989 \\ 1.28402771 \end{array} \right) \end{equation}

\begin{equation} eigenvectors=\left( \begin{array}{cc} -.735178656 & -.677873399 \\ .677873399 & -.735178656 \end{array} \right) \end{equation}

上面是两个特征值，下面是对应的特征向量，特征值0.0490833989对应特征向量为$(-0.735178656,0.677873399)^T$，这里的特征向量都归一化为单位向量。

第四步，将特征值按照从大到小的顺序排序，选择其中最大的$k$个，然后将其对应的$k$个特征向量分别作为列向量组成特征向量矩阵。

这里特征值只有两个，我们选择其中最大的那个，这里是1.28402771，对应的特征向量是$(-0.677873399,-0.735178656)^T$。

第五步，将样本点投影到选取的特征向量上。假设样例数为$m$，特征数为$n$，减去均值后的样本矩阵为$DataAdjust(m \times n)$，协方差矩阵是$n \times n$，选取的$k$个特征向量组成的矩阵为$EigenVectors(n \times k)$。那么投影后的数据FinalData为:

\begin{equation} FinalData(m \times k) = DataAdjust(m \times n) EigenVectors(n \times k) \end{equation}

于是我们得到结果:

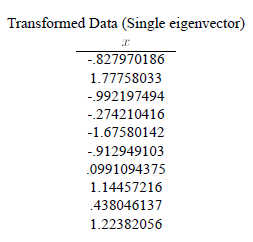
这样，就将原始样例的$n$维特征变成了$k$维，这$k$维就是原始特征在$k$维上的投影。上面的数据可以认为是learn和study特征融合为一个新的特征叫做LS特征，该特征基本上代表了这两个特征。这样PCA的过程基本结束。在第一步减均值之后，其实应该还有一步对特征做方差归一化。比如一个特征是汽车速度（0到100），一个是汽车的座位数（2到6），显然第二个的方差比第一个小。因此，如果样本特征中存在这种情况，那么在第一步之后，求每个特征的标准差$\sigma$，然后对每个样例在该特征下的数据除以$\sigma$。

归纳一下，使用我们之前熟悉的表示方法，在求协方差之前的步骤是：

1. Let $\mu = {1 \over m}\sum_{i=1}^m x^{(i)}$;
2. Replace each $x^{(i)}$ with $x^{(i)}-\mu$;
3. Let $\sigma_j^2 = {1 \over m}\sum_i (x_j^{(i)})^2$;
4. Replace each $x_j^{i}$ with $x_j^{i}/\sigma_j$.

其中$x^{(i)}$是样例，共$m$个，每个样例$n$个特征，也就是说$x^{(i)}$是$n$维向量。$x_j^{(i)}$是第$i$个样例的第$j$个特征。$\mu$是样例均值。$\sigma_j$是第$j$个特征的标准差。

整个PCA过程貌似及其简单，就是求协方差的特征值和特征向量，然后做数据转换。但是有没有觉得很神奇，为什么求协方差的特征向量就是最理想的$k$维向量？其背后隐藏的意义是什么？整个PCA的意义是什么？

PCA理论基础

要解释为什么协方差矩阵的特征向量就是$k$维理想特征，我看到的有三个理论：分别是最大方差理论、最小错误理论和坐标轴相关度理论。这里简单探讨前两种，最后一种在讨论PCA意义时简单概述。

最大方差理论

在信号处理中认为信号具有较大的方差，噪声有较小的方差，信噪比就是信号与噪声的方差比，越大越好。因此我们认为，最好的$k$维特征是将$n$维样本点转换为$k$维后，每一维上的样本方差都很大。

比如下图有5个样本点：（已经做过预处理，均值为0，特征方差归一）

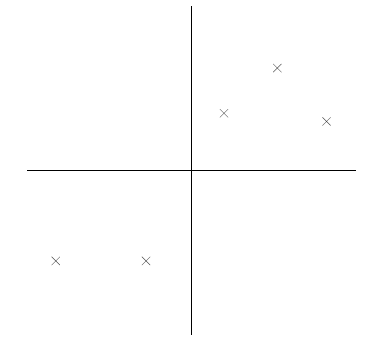
下面将样本投影到某一维上，这里用一条过原点的直线表示（预处理的过程实质是将原点移到样本点的中心点）。

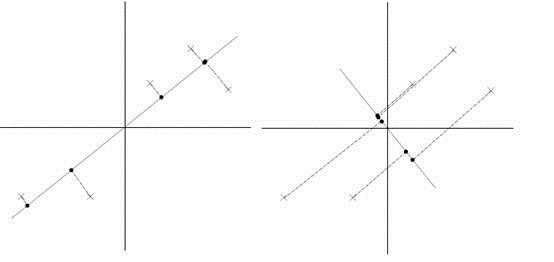
假设我们选择两条不同的直线做投影，那么左右两条中哪个好呢？根据我们之前的方差最大化理论，左边的好，因为投影后的样本点之间方差最大。

这里先解释一下投影的概念：

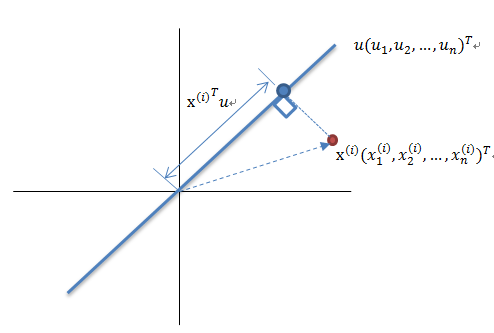
红色点表示样例$x^{(i)}$，蓝色点表示$x^{(i)}$在$u$上的投影，$u$是直线的斜率也是直线的方向向量，而且是单位向量。蓝色点是示$x^{(i)}$在$u$上的投影点，离原点的距离是${x^{(i)}}^Tu$或$u^Tx^{(i)}$.由于这些样本点（样例）的每一维特征均值都为0，因此投影到$u$上的样本点（只有一个到原点的距离值）的均值仍然是0。

回到上面左右图中的左图，我们要求的是最佳的$u$，使得投影后的样本点方差最大。

由于投影后均值为0，因此方差为：

\begin{equation} \begin{split} {1 \over m}\sum_{i=1}^m ({x^{(i)}}^Tu)^2 &= {1 \over m}\sum_{i=1}^m u^Tx^{(i)}{x^{(i)}}^Tu \\ &= u^T ({1 \over m}\sum_{i=1}^m x^{(i)}{x^{(i)}}^T)u. \end{split} \end{equation}

中间那部分很熟悉啊，不就是样本特征的协方差矩阵么（$x^{(i)}$的均值为0，一般协方差矩阵都除以$m-1$，这里用$m$）。

用$\lambda$来表示${1 \over m}\sum_{i=1}^m ({x^{(i)}}^Tu)^2$，$\Sigma$表示${1 \over m}\sum_{i=1}^m x^{(i)}{x^{(i)}}^T$，那么上式可写作:

\begin{equation} \lambda = u^T \Sigma u \end{equation}

由于$u$是单位向量，即$u^Tu=1$，上式两边都左乘$u$得，$u\lambda = \lambda u = uu^T \Sigma u$

即$\Sigma u = \lambda u$

We got it！$\lambda$就是$\Sigma$的特征值，$u$是特征向量。最佳的投影直线是特征值$\lambda$最大时对应的特征向量，其次是$\lambda$第二大对应的特征向量，依次类推。

因此，我们只需要对协方差矩阵进行特征值分解，得到的前$k$大特征值对应的特征向量就是最佳的$k$维新特征，而且这$k$维新特征是正交的。得到前$k$个$u$以后，样例$x^{(i)}$通过以下变换可以得到新的样本。

\begin{equation} y^{(i)} = \left[ \begin{array}{cc} u_1^Tx^{(i)} \\ u_2^Tx^{(i)} \\ ... \\ u_k^Tx^{(i)} \end{array} \right] \in R^k \end{equation}

其中的第$j$维就是$x^{(i)}$在$u_j$上的投影。通过选取最大的$k$个$u$，使得方差较小的特征（如噪声）被丢弃。

最小平方误差理论

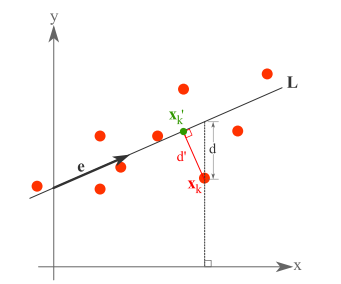
假设有这样的二维样本点（红色点），回顾我们前面探讨的是求一条直线，使得样本点投影到直线上的点的方差最大。本质是求直线，那么度量直线求的好不好，不仅仅只有方差最大化的方法。再回想我们学过的线性回归等，目的也是求一个线性函数使得直线能够最佳拟合样本点，那么我们能不能认为最佳的直线就是回归后的直线呢？回归时我们的最小二乘法度量的是样本点到直线的坐标轴距离。比如这个问题中，特征是$x$，类标签是$y$。回归时最小二乘法度量的是距离$d$。如果使用回归方法来度量最佳直线，那么就是直接在原始样本上做回归了，跟特征选择就没什么关系了。

因此，我们打算选用另外一种评价直线好坏的方法，使用点到直线的距离$d\prime$来度量。

现在有$n$个样本点$(x_1,x_2,\dots,x_n)$，每个样本点为$m$维（这节内容中使用的符号与上面的不太一致，需要重新理解符号的意义）。将样本点$x_k$在直线上的投影记为$x_k \prime$，那么我们就是要最小化

\begin{equation} \sum_{k=1}^n ||x_k \prime - x_k||^2 \end{equation}

这个公式称作最小平方误差（Least Squared Error）。

而确定一条直线，一般只需要确定一个点，并且确定方向即可。

第一步确定点：

假设要在空间中找一点$x_0$来代表这$n$个样本点，“代表”这个词不是量化的，因此要量化的话，我们就是要找一个$m$维的点$x_0$，使得

\begin{equation} J_0(x_0) = \sum_{k=1}^n ||x_0-x_k||^2 \end{equation}

最小。其中$J_0(x_0)$是平方错误评价函数（squared-error criterion function).对$x_0$求偏导易知:

\begin{equation} x_0 = \sum_{k=1}^n x_k \end{equation}

第二步确定方向:

我们从$x_0$拉出要求的直线，假设直线的方向是单位向量$e$。那么直线上任意一点，比如$x_k \prime$就可以用点$x_0$和$e$来表示

\begin{equation} x_k \prime = x_0 + a_k e \end{equation}

其中$a_k$是$x_k \prime$到点$x_0$的距离。

我们重新定义最小平方误差：

\begin{equation} J_1(a_1,\dots,a_n,e) = \sum_{k=1}^n ||x_k \prime - x_k||^2 = \sum_{k=1}^n ||(x_0+a_ke)-x_k)||^2 \end{equation}

这里的$k$只是相当于$i$。$J_1$就是最小平方误差函数，其中的未知参数是$a_1,\dots,a_n$和$e$。

实际上是求$J_1$的最小值。首先将上式展开：

\begin{equation} \begin{split} J_1(a_1,\dots,a_n,e) &= \sum_{k=1}^n ||(x_0+a_ke)-x_k)||^2 = \sum_{k=1}^n ||a_ke-(x_k-x_0)||^2 \\ &= \sum_{k=1}^n a_k^2||e||^2 - 2\sum_{k=1}^n a_ke^T(x_k-x_0)+ \sum_{k=1}^n ||x_k-x_0||^2 \end{split} \end{equation}

我们首先固定$e$，将其看做是常量,$||e||^2 = 1$，然后对$a_k$进行求导，得:

\begin{equation} a_k = e^T(x_k-x_0) \end{equation}

这个结果意思是说，如果知道了$e$，那么将$x_k-x_0$与$e$做内积，就可以知道了$x_k$在$e$上的投影离$x_0$的长度距离，不过这个结果不用求都知道。

然后是固定$a_k$，对$e$求偏导数，我们先将上式代入$J_1$，得

\begin{equation} \begin{split} J_1(e) &= \sum_{k=1}^n a_k^2||e||^2 - 2\sum_{k=1}^n a_k^2 + \sum_{k=1}^n ||x_k -x_0||^2 \\ &= -\sum_{k=1}^n [e^T(x_k-x_0)]^2 + \sum_{k=1}^n ||x_k - x_0 ||^2 \\ &= -\sum_{k=1}^n e^T (x_k-x_0)(x_k-x_0)^T e + \sum_{k=1}^n ||x_k - x_0 ||^2 \\ &= -e^TSe+\sum_{k=1}^n ||x_k-x_0||^2 \end{split} \end{equation}

其中$S=\sum_{k=1}^n (x_k-x_0)(x_k-x_0)^T$与协方差矩阵类似，只是缺少个分母$n-1$，我们称之为散列矩阵（scatter matrix）。

然后可以对$e$求偏导数，但是$e$需要首先满足$e^Te=1$，引入拉格朗日乘子$\lambda$，来使$e^TSe$最大（$J_1$最小），令:

\begin{equation} u = e^TSe - \lambda(e^Te-1) \end{equation}

求偏导:

\begin{equation} \frac{\partial u}{\partial e} = 2Se - 2\lambda e = 0 \end{equation}

于是我们有:

\begin{equation} Se = \lambda e \end{equation}

两边除以$n-1$就变成了，对协方差矩阵求特征值向量了。

从不同的思路出发，最后得到同一个结果，对协方差矩阵求特征向量，求得后特征向量上就成为了新的坐标，如下图：

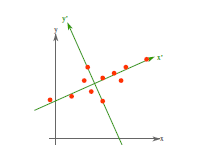
这时候点都聚集在新的坐标轴周围，因为我们使用的最小平方误差的意义就在此。

NOTE:

PCA技术的一大好处是对数据进行降维的处理。我们可以对新求出的“主元”向量的重要性进行排序，根据需要取前面最重要的部分，将后面的维数省去，可以达到降维从而简化模型或是对数据进行压缩的效果。同时最大程度的保持了原有数据的信息。

SVD分解

以上我们介绍了获得PCA solution的两种方法，现我们提供基于奇异值分解(Singular Value Decomposition)另一种方法.任一$N \times D$矩阵$X$均可分解为如下形式:

\begin{equation} X = USV^T \end{equation}

其中,$U$是一$N \times N$矩阵,其列向量均正交(即$U^TU = I_N$),$V$是一$D \times D$矩阵且行列向量均正交（即$V^TV = VV^T = I_D$,$S$为一$N \times D$矩阵，其主对角线上包含$r = min(N,D)$奇异值$\sigma_i \geq 0$(Why?),其余则由0填充。如下图中(a)所示：

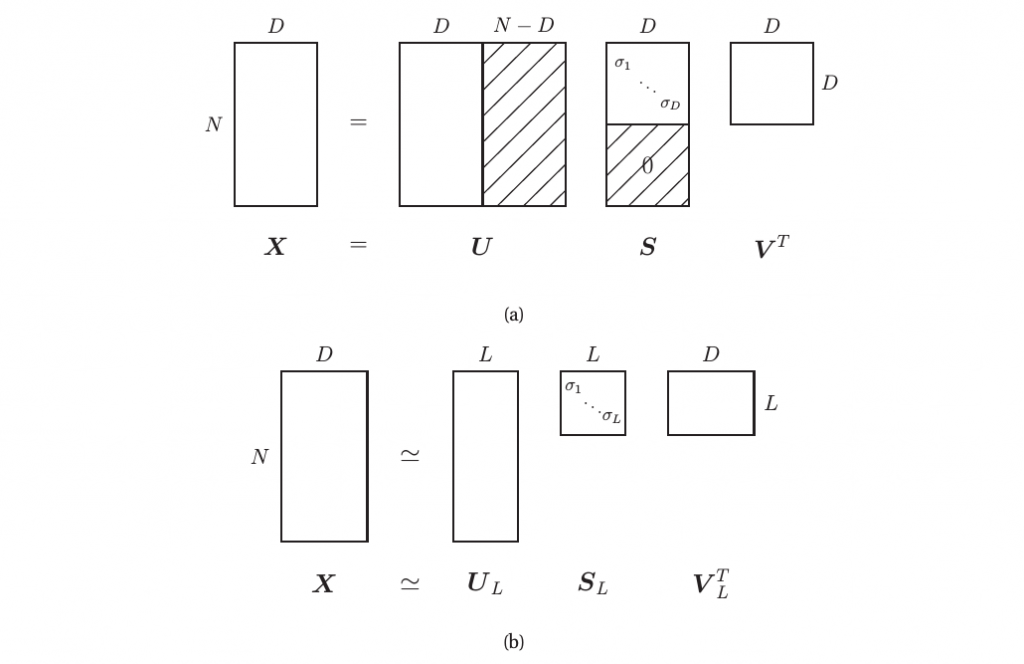
假定$N>D$,则最多有$D$个奇异值；$U$右边的$N-D$行由于与$0$相乘，所以是无关项，于是我们得到的Economy sized SVD或者Thin SVD避免了对于这些无关元素的计算，可被表示为如下形式：若$N>D$,我们有：

\begin{equation} X = \hat{U} \hat{S} \hat{V}^T \end{equation}

其中$\hat{S}$为$D \times D$矩阵，$\hat{V}$为$D \times D$矩阵。

若$N<D$,此时$\hat{U}$为$N \times N$矩阵，$\hat{S}$为$N \times N$矩阵，$\hat{V}$为$N \times D$矩阵。

以下正式开始我们对PCA solution的推导：

若$X = USV^T$,则有:

\begin{equation} X^TX = VS^TU^TUSV^T = V(S^TS)V^T = VDV^T \end{equation}

其中$D=S^2$是包含奇异值平方的对角阵。于是有：$(X^TX)V = VD$

故$V$为$X^TX$的特征向量集合，$D$为$X^TX$的特征值集合(奇异值的平方)。对$XX^T$也能得到类似的结果。

实际上,PCA的过程实际上是取$S$中最大的若干特征值(为了降维，我们并不是取所有的特征值）然后重新构造原矩阵的过程，即PCA只是对于原矩阵的低秩近似。

---

TODO Board:

• Kernel-PCA
• Probablistic PCA
• 如何确定隐含变量空间的维度
• ICA

参考文献

---

1. 因子分析（Factor Analysis)
2. Expectation–maximization algorithm
3. 主成分分析（Principal components analysis)-最大方差解释
4. 主成分分析（Principal components analysis）-最小平方误差解释
5. Machine Learning:A Probablistic Perspective Chapter 12
6. 独立成分分析（Independent Component Analysis)

Comment

---